Взвешивание Земли

Чтобы взвешивать планеты, прежде всего мы должны взвесить нашу Землю. Архимед сказал, что если бы у него была точка опоры, он мог бы сдвинуть Землю с помощью рычагов. С таким же успехом он мог бы взвесить Землю, наблюдая, насколько легко она сдвигается, когда он нажимает на рычаг. В действительности нам необходимо знать не вес Земли, но её массу. Вес тела есть только мера притяжения его Землёй, тогда как масса тела характеризует количество содержащейся в нём материи. Одно из великих открытий Ньютона заключалось в установлении факта, что вес тела пропорционален его массе. Если мы вернёмся к законам движения Ньютона, то увидим, что масса представляет собой меру силы, необходимой для изменения скорости движения тела на некоторую величину. Сдвинуть десятитонный вагон труднее, чем детскую коляску, вследствие разницы в массе. В пустом пространстве, где нет никаких притягивающих тел, ни вагон, ни детская коляска не будут иметь никакого веса, но массы их останутся неизменными.

Мы точно знаем, с какой силой действует притяжение Земли на единицу массы. Эта сила есть сила тяжести на поверхности Земли, которая притягивает нас к Земле и позволяет нам взвешивать различные предметы. Поскольку сила тяжести пропорциональна массе Земли, единственной неизвестной величиной является постоянная притяжения между двумя массами, так называемая постоянная тяготения (Закон всемирного тяготения Ньютона утверждает, что два тела с массами m₁ и m₂, находящиеся на расстоянии r друг от друга, взаимно притягиваются с силой F=γm₁•m₂/r², где γ - постоянная тяготения)).

Один из методов определения этой постоянной заключается в измерении притяжения горы по отклонению линии отвеса. Как показано на рис. 30, линия отвеса направлена не строго вертикально, а отклонена от горы на некоторый угол, так как грузик отвеса притягивается к горе. Таким образом мы измеряем силу, с которой гора действует на грузик, и определяем массу горы, зная её размеры и составляющие её породы. Поскольку расстояние до горы измерить легко, мы имеем все данные для вычисления постоянной тяготения, а следовательно, и массы Земли.

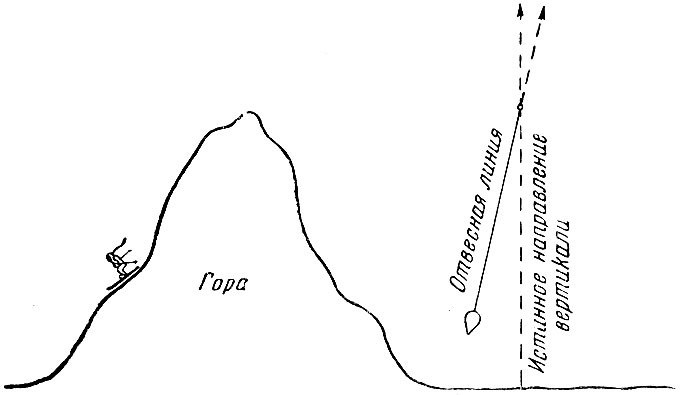
Рис. 30. Гора притягивает свинцовый грузик. Направление отвеса отклоняется от вертикали, давая меру притяжения горы

Описанный метод весьма прост, но менее точен, чем лабораторные методы. С помощью весьма чувствительных инструментов можно непосредственно измерить притяжение, которое оказывает большой свинцовый шар на такой же шар меньших размеров, и таким образом получить значение постоянной тяготения. Поскольку вес малого шара измеряет величину притяжения его Землёй, массу Земли можно выразить в массах большого шара, применяя закон тяготения. Если бы Землю можно было положить на весы на её поверхности, то она весила бы 6 600 000 000 000 000 000 000 т.

Сила тяготения, есть лишь небольшое отклонение от отсутствия всякой силы; она становится заметной, лишь когда мы имеем дело с огромными количествами материи. Представим себе шар, сделанный из всего золота добытого во всём мире, скажем, 30000 т; такой шар имел бы 14 м в диаметре. Если бы этот шар находился в пространстве, вдали от всех притягивающих сил, то человек весом 80 кг, сидящий на нём, весил бы столько же, сколько 0,3 г на Земле. Сверчок легко мог бы поднять этого человека, а лягушка могла бы вообще сбросить его с золотого шара. Поскольку обычно человека не так легко отогнать от золота, мы можем заключить, подобно Эзопу, что сила скупости значительно превосходит силу тяготения.