Расстояние до Солнца

Измеряя положение планет или астероидов и применяя закон Ньютона, астрономы могут вычислить орбиты, по которым планеты обращаются вокруг Солнца, и предсказать положения планет на будущее время с высокой степенью точности. Относительные расстояния могут быть определены с такой же точностью, с какой это удаётся сделать при самых точных измерениях расстояний на Земле, т. е. с точностью до одной миллионной. Необычная трудность заключается в том, что все эти точные расстояния выражены в астрономических единицах, т. е. в средних расстояниях от Земли до Солнца, а не в метрах или километрах. Для предвычис-ления положений светил эта неопределённость почти не имеет значения, но никакой учёный не согласится пользоваться измерительной линейкой неизвестной длины.

При измерении астрономической единицы мы сталкиваемся с тем затруднением, что наибольшая доступная нам единица измерения есть сама Земля; её размеры в настоящее время известны довольно точно. Но радиус Земли составляет менее 1/20000 астрономической единицы. Если смотреть с Солнца, то радиус Земли будет виден под углом всего 8,80 секунды дуги; этот угол-геоцентрический параллакс (Геоцентрическим параллаксом какого-либо небесного объекта называется угол, под которым виден радиус Земли, перпендикулярный к лучу зрения, если смотреть с этого объекта. Геоцентрический параллакс не следует смешивать с годичным параллаксом, для которого базисом является астрономическая единица)) Солнца (рис. 28). Хотя параллакс Солнца можно измерить, производя два одновременных наблюдения на двух далеко отстоящих друг от друга станциях, но самый угол настолько мал, что относительная ошибка будет весьма велика; поэтому точное определение длины астрономической единицы не может быть достигнуто с помощью измерений положения Солнца.

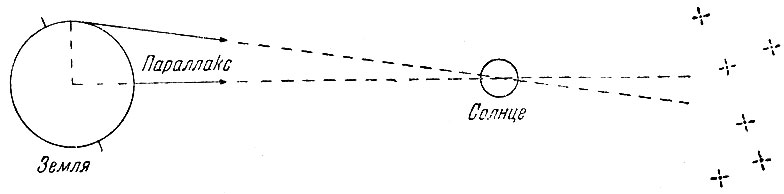
Рис. 28. Геоцентрический параллакс Солнца. Геоцентрическим параллаксом какого-либо небесного тела называется угол, под которым виден радиус Земли, если смотреть с этого тела

Более приемлемый способ заключается в измерении в километрах расстояния до какого-либо небесного тела, которое подходит близко к Земле. Поскольку расстояние этого тела в астрономических единицах нам известно, так как орбита его точно вычислена, то мы можем сравнить между собой обе эти величины и найти таким образом, сколько километров заключается в астрономической единице. Луна не годится для этой цели, так как её расстояние нельзя измерить в астрономических единицах, не пользуясь при расчётах величиной массы Земли. Марс при наиболее благоприятных условиях подходит к Земле лишь на расстояние 55 670000 км. Венера подходит ближе, на 41 840 000 км, но в это время она видна почти в направлении Солнца и точных измерений произвести нельзя (см. рис. 4). Наиболее подходящим объектом для решения поставленной задачи является астероид Эрос.

Весьма приятно найти какое-то полезное применение для астероида, так как в астрономии астероиды обычно только мешают, а не помогают. Когда Эрос подходит к Земле на расстояние 22 500000 км, то его параллакс в 7 раз больше солнечного, т. е. несколько больше минуты. Этот астероид представляется наблюдателю и выходит на фотографиях, как звезда или как светящаяся точка; поэтому измерения его легко осуществимы и очень точны. Вместо того чтобы производить наблюдения одновременно в двух различных местах земного шара, наблюдатели могут работать независимо один от другого; просто каждый из них выжидает, пока Земля повернётся, и фотографирует астероид вечером, в полночь и утром, как показано на рис. 29. Положение Эроса среди звёзд меняется в зависимости от изменения положения наблюдателя на Земле. Зная момент времени, когда был сделан каждый снимок и своё точное положение на Земле, наблюдатель может вычислить расстояние до Эроса в километрах совершенно с такой же точностью, как если бы были произведены два одновременных наблюдения в двух различных точках земного шара. Этот процесс аналогичен измерению какого-либо небольшого расстояния с помощью одного глаза, когда наблюдатель поворачивает голову или двигает ей из стороны в сторону.

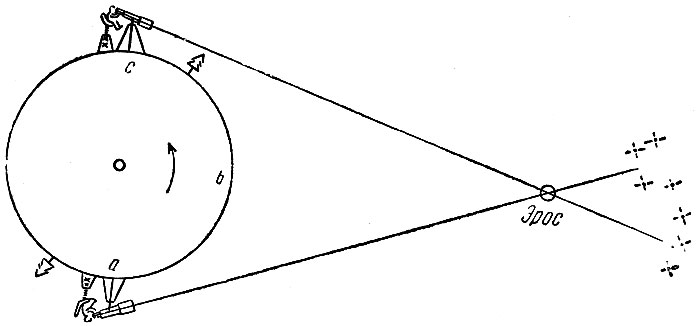
Рис. 29. Измерение расстояния до Эроса. Вращением Земли наблюдатель переносится из 'а' в 'с' и таким образом может измерить параллакс Эроса

Главная поправка, которую приходится при этом вводить, обусловлена движением Эроса по небу в промежутке между наблюдениями. Когда эта поправка и прочие, более мелкие, введены, расстояние может быть определено очень точно. В январе 1931 г. имело место одно из наибольших приближений Эроса к Земле (на расстояние 26 000000 км).

Сотрудничество главных обсерваторий мира явилось важнейшим условием наилучшего определения расстояния от Земли до Эроса. Ещё до приближения астероида были произведены повторные наблюдения многих звёзд, расположенных вдоль его орбиты, чтобы получить более точные опорные точки для определения видимого направления к Эросу. Измерялись даже цвета звёзд, чтобы ввести поправку на небольшой преломляющий эффект земной атмосферы. Были изготовлены специальные объективы и сконструированы специальные камеры для получения наиболее эффективных снимков. После этих тщательных приготовлений было получено много сотен снимков на различных обсерваториях, разбросанных по всему земному шару.

Однако подготовка и выполнение программы наблюдений не составляли главной части работы, необходимой для разрешения поставленной задачи. Измерения и редукция множества пластинок и связанные с этим разнообразнейшие вычисления требуют ещё большей затраты труда и времени. Предварительные результаты проведённого исследования, согласованные со старыми результатами, полученными различными другими методами, дают для солнечного параллакса величину 8", 803. Тогда астрономическая единица будет равна 149 430000 км с вероятной ошибкой около 16 000 км. С первого взгляда эта ошибка может показаться большой, но, в конце концов, она представляет собой лишь 1/10000 измеренной величины и потому на самом деле она сравнительно невелика.