Марс как планета

Первые наблюдения Марса проводились еще до изобретения телескопа. Это были позиционные наблюдения. Их целью было определение точных положений планеты по отношению к звездам. Такие наблюдения проводил еще Коперник, стараясь подкрепить ими свою гелиоцентрическую систему мира. Точность наблюдений Коперника составляла около одной минуты дуги.

Значительно более точными были наблюдения знаменитого датского астронома Тихо Браге; их точность доходила до 10 секунд дуги. За свою долгую жизнь Тихо пронаблюдал десять противостояний Марса, накопив непрерывный ряд наблюдений за 22 года. Этот ценнейший материал попал после смерти Тихо в самые верные руки - в руки Иоганна Кеплера, прекрасного вычислителя, человека широких взглядов, не связывавшего себя привычными в те времена представлениями о движении планет по окружностям - самым "совершенным" из всех кривых. Обработка наблюдений положений Марса, выполненных Тихо Браге, привела Кеплера к открытию трех его знаменитых законов движения планет. Истинной формой планетных орбит оказался эллипс, а Солнце находилось в одном из фокусов этого эллипса (общем для всех планет).

Как хорошо, что для выяснения законов движений планет и формы их орбит был выбран именно Марс, а, скажем, не Венера. Орбита Марса имеет эксцентриситет 0,093, тогда как орбита Венеры - только 0,007, в 13 раз меньше. Быть может, имея дело с наблюдениями Венеры или Юпитера, Кеплер не открыл бы свой первый закон, не обнаружил бы отличия орбиты планеты от окружности.

И все же выбор Марса не был делом случая. Наблюдать Венеру (а тем более Меркурий) очень трудно, так как эта планета не отходит от Солнца далее 48°, наблюдается на светлом небе и ее положение трудно привязывать к положениям неподвижных звезд. С другой стороны, Юпитер и Сатурн движутся по небу очень медленно, так как находятся относительно далеко от Земли. Марс же близок к Земле, сравнительно быстро перемещается среди звезд, его можно наблюдать на фоне звездного неба на любых угловых расстояниях от Солнца, он описывает довольно широкие петли около эпохи противостояния.

Элементы орбиты Марса, найденные Кеплером, мало отличались от современных. Например, большая полуось орбиты по Кеплеру равнялась 1,5264 астрономической единицы (а. е.), тогда как современное ее значение 1,5237 а. е. Эксцентриситет орбиты Марса по Кеплеру равен 0,0926, а современное его значение 0,0934.

Уже из приведенных чисел видно, что Марс расположен от Солнца в полтора раза дальше Земли, и, значит, получает от Солнца в 2,3 (1,522) раза меньше света и тепла. Расстояние Марса от Солнца составляет в среднем 228 млн. км, тогда как Земля отстоит от дневного светила на 150 млн. км (рис. 1).

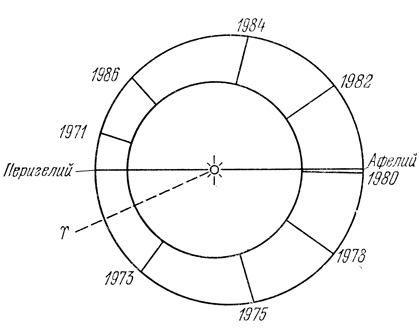
Рис. 1. Орбиты Марса и Земли. Указаны годы противостояний Марса

Благодаря большому эксцентриситету орбиты Марс может изменять свое расстояние от Солнца в довольно широких пределах. Чтобы найти, на сколько расстояние в ближайшей к Солнцу точке орбиты, перигелии, меньше среднего, надо помножить среднее расстояние на эксцентриситет. Получим:

На столько же дальше среднего наибольшее расстояние Марса от Солнца в самой далекой точке его орбиты (в афелии).

Следовательно, кратчайшее расстояние Марса от Солнца равно 207 млн. км, а наибольшее - 249 млн. км. Эти величины относятся как 1:1,2, а поток солнечного света и тепла на единицу поверхности Марса в перигелии и афелии как 1,44:1.

Чтобы понять, как может изменяться положение Марса относительно Земли, рассмотрим основные конфигурации этой планеты (они справедливы и для других верхних планет, от Юпитера до Плутона).

Пусть Земля при движении по орбите вокруг Солнца S находится в положении T (рис. 2). На орбите Марса отметим четыре важных положения планеты: соединение K, когда планета находится за Солнцем, на продолжении прямой TS, квадратуры Q₁ и Q₂, когда угол между направлениями на Солнце и планету (∠STQ₁=∠STQ₂) равен 90°, и противостояние О, когда планета находится снова на продолжении прямой TS, но в направлении, противоположном Солнцу (отсюда и выражение "противостояние").

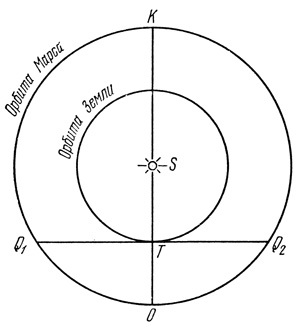
Рис. 2. Конфигурации Марса. S - Солнце, T - Земля, O - противостояние, K - соединение, Q₁ и Q₂ - квадратуры

Легко видеть, что именно в противостоянии планета расположена ближе всего к Земле, а в соединении расстояние между ними максимально. Поэтому эпоха соединения - самый неблагоприятный период для наблюдений Марса, а эпоха противостояния, наоборот, самый благоприятный. И не только благодаря близости планеты к Земле, но и потому, что в это время планета видна всю ночь, восходит с заходом Солнца и заходит с его восходом.

Прежде чем перейти к более подробному рассмотрению условий видимости Марса во время противостояний, остановимся на значении квадратур. Обычно думают, что ничего особенного эти конфигурации планеты не представляют, за исключением того, что планета находится на 90° от Солнца. На самом деле это не так. Квадратуры замечательны в двух отношениях: во-первых, в это время скорость приближения планеты к Земле или удаления от нее максимальна, во-вторых, угол фазы планеты достигает в квадратурах наибольшего значения.

Поясним эти два обстоятельства. Движение планеты относительно Земли по лучу зрения используется спектроскопистами для отделения с помощью эффекта Доплера спектральных линий планетного происхождения от так называемых теллурических линий, вызванных поглощением света газами земной атмосферы. Найдем, чему равна эта радиальная скорость (по лучу зрения) для внешней планеты. Пусть Земля (рис. 3) находится в точке T и движется по орбите со скоростью v_t=30 км/сек, а Марс - в точке М и движется со средней скоростью v_m=24 км/сек. Пусть векторы скоростей v_t и v_m образуют с лучом зрения MT углы α и β соответственно. Тогда очевидно, что радиальная скорость v_r будет равна разности проекций v_t и v_m на направление TM:

Угол α=L - 90°^*, где L - угловое расстояние Марса от Солнца S (скорость Земли направлена по касательной, которая перпендикулярна к радиусу ST в точке касания Т). Угол β=90° - P, где P - угол фазы, т. е. угол между направлениями планета - Солнце и планета - Земля. Кроме того, из треугольника SMT по теореме синусов имеем

где r_t и r_m - расстояния Земли и Марса от Солнца. Отсюда сразу видно, что угол фазы P достигает наибольшего значения, когда L=90°, т. е. во время квадратур. В это время P=41° (если Марс находится на среднем расстоянии) или P=47° (если Марс в перигелии). Фаза (или доля освещенного диска) Марса равна при этом 0,84. Мы можем заменить α и β на L и P и преобразовать формулу (1) так:

^* (Или 90° - L, если Марс находится по другую сторону от точки Q.)

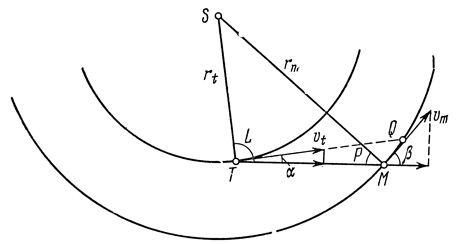
Рис. 3. К расчету радиальных скоростей Марса относительно Земли

Величина в скобке (для средних значений r_m и v_m) равна 14 км/сек. Очевидно, что при L=90° vr тоже достигает этого значения, которое является максимальным^*.

^* (Впрочем, если Марс в эпоху квадратуры находится в афелии, его радиальная скорость может достигнуть 17 км/сек.)

Обратимся теперь к противостояниям Марса. По условиям видимости планеты не все они равноценны по двум причинам. Во-первых, из-за эксцентриситета орбиты Марса его расстояние от Земли в момент противостояния может меняться от 56 до 100 млн. км. Во-вторых, склонение, а значит, и высота планеты над горизонтом различны для разных противостояний.

Те противостояния, при которых расстояние до Марса не превышает 60 млн. км, принято называть великими. Очевидно, в период великих противостояний Марс должен быть вблизи перигелия. Если соединить перигелий орбиты Марса с Солнцем прямой линией, то она пересечет орбиту Земли в той точке, которую Земля проходит 29 августа. Поэтому даты великих противостояний Марса приходятся обычно на август или сентябрь (исключением был 1939 г., когда великое противостояние наступило 23 июля).

В следующей таблице приведены даты великих противостояний за последние 100 лет и кратчайшие расстояния Марса от Земли в астрономических единицах и в миллионах километров.

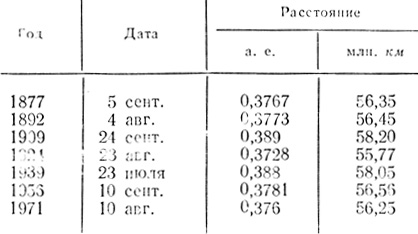
Даты великих противостояний за последние 100 лет

Сразу видно, что великие противостояния следуют с интервалом в 15 или 17 лет. Чтобы понять существующую здесь закономерность, вспомним, что период обращения Марса вокруг Солнца равен 687 суткам. Синодический период планеты, т. е. интервал от одного противостояния до следующего, определяется по формуле

где P=687 сут. - год Марса, T=365,25 сут. - год Земли. Из этой формулы находим S=780 суткам, т. е. синодический период Марса равен 2 годам 50 суткам. Но это - только среднее значение. Из-за эксцентриситета орбиты Марса синодический период меняется в пределах от 764 до 811 суток, как можно видеть из следующей таблички последовательных противостояний Марса с 1956 по 1975 г.

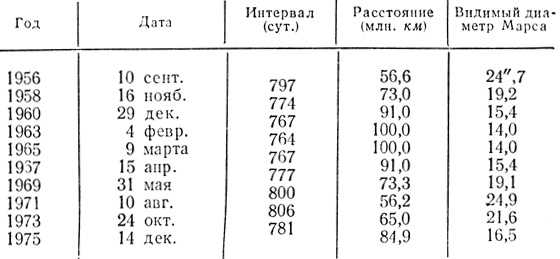
Последовательных противостояний Марса с 1956 по 1975 г

В табличке приведены также значения наименьшего расстояния Марса от Земли в эпоху противостояния и наибольшего видимого диаметра Марса в секундах дуги. Из последнего столбца видно, какие преимущества представляют великие противостояния по сравнению с "обычными".

Но великие противостояния имеют, с точки зрения условий наблюдений, и свои минусы, особенно для обсерваторий и наблюдателей средних широт северного полушария. В это время Марс имеет большое южное склонение и находится очень низко над горизонтом, наблюдать его неудобно. Так, во время великого противостояния 10 августа 1971 г. склонение Марса было -22° и на широте +50° он даже в кульминации не поднимался выше 18 градусов над горизонтом! Наблюдения Марса в это время велись на южных обсерваториях Советского Союза, Европы, США, Японии и на обсерваториях южного полушария.

С этой точки зрения "не великое" противостояние 24 октября 1973 г. для наблюдателей средних широт было более выгодно: хотя диск Марса был несколько меньше, чем в 1971 г. (2″,6 против 24″,9), зато склонение планеты было около +9°, и ее высота в кульминации на той же широте достигала 49 градусов.

Ознакомившись с орбитой и условиями видимости Марса, обратимся к свойствам Марса как планеты: его размерам, массе, вращению.

Экваториальный диаметр Марса равен, по новейшим определениям французского астронома О. Дольфюса, 6790 км, т. е. 0,53 земного. Полярный диаметр Марса несколько меньше экваториального из-за полярного сжатия. Разность экваториального и полярного радиусов Марса равна 1/191 его экваториального радиуса. У Земли эта величина равна 1/298. Иначе говоря, Марс сплюснут у полюсов несколько сильнее, чем Земля^*.

^* (Данные "Маринера-9" позволили уточнить наши сведения о форме и размерах Марса. Фигура планеты близка к трехосному эллипсоиду, причем наибольший экваториальный диаметр уровенной поверхности (соответствующей у нас на Земле уровню мирового океана) равен 6788 км, наименьший - 6786 км, полярный диаметр 6753 км. Истинная поверхность Марса отличается от уровенной: для истинной поверхности эти три диаметра равны соответственно 6802, 6790 и 6745 км, т. е. сжатие истинной поверхности больше.)

Марс вращается вокруг своей оси почти так же, как и Земля: его период вращения равен 24 час. 37 мин. 23 сек., что на 41 мин. 19 сек. больше периода вращения Земли. Ось вращения наклонена к плоскости орбиты планеты на угол 65°, почти равный углу наклона земной оси (66°,5). Это значит, что смена дня и ночи, а также смена времен года на Марсе протекает почти так же, как на Земле. Там есть и тепловые пояса, подобные земным: тропический (широта тропиков ±25°), два умеренных и два полярных (широта полярных кругов ±65°).

Но есть и отличия. Прежде всего из-за удаленности от Солнца климат Марса вообще суровее земного. Далее, год Марса (687 земных суток или 668 марсианских суток) почти вдвое длиннее земного, а значит, дольше длятся и сезоны. Наконец, из-за эксцентриситета орбиты длительность и характер сезонов заметно отличаются в северном и южном полушариях планеты, как видно из следующей таблички:

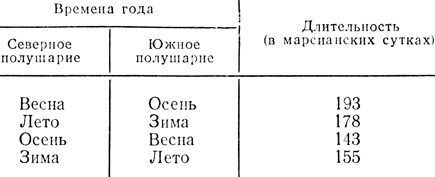
Таблица

Таким образом, в северном полушарии планеты лето долгое, но прохладное, а зима короткая и мягкая (Марс в это время близок к перигелию), тогда как в южном полушарии лето короткое, но теплое, а зима долгая и суровая. Как все это выражается в привычных нам температурах, мы узнаем дальше.

Масса Марса была довольно точно определена по движению его спутников Фобоса и Деймоса, а теперь уточнена по движению искусственных спутников серии "Маринер". Она равна 1:3098700 доле массы Солнца, или 0,107 массы Земли, или 6,42·10²⁶ г. Отсюда средняя плотность Марса получается 3,89 г/см³ (0,70 средней плотности Земли), ускорение силы тяжести на его поверхности на экваторе 372 см/сек² (0,38 земного) и критическая скорость, достаточная для преодоления притяжения планеты, 5,0 км/сек (против 11,2 км/сек на Земле).

Таковы общие характеристики Марса как планеты. Как мы не раз еще сможем убедиться, они во многом определяют условия на Марсе: состояние его атмосферы, климат, ветровой режим. Но расскажем обо всем по порядку.