2. Почему солнечная система не распадается

Могущественная, всё подчиняющая себе сила даёт возможность Солнцу удерживать планеты на их орбитах и благодаря той же силе планеты в состоянии удержать своих спутников. Открытие закона всемирного тяготения, описывающего эту силу, явилось блестящим достижением человеческой мысли. Великий учёный Исаак Ньютон, исходя из данных наблюдений и теорий своего времени, развил новую отрасль математики для решения динамических задач и, наконец, объединил наблюдения и математическую теорию, сформулировав простой, но универсальный закон. Мы лучше оценим всё сделанное Ньютоном, если бросим взгляд назад, на тот уровень научного знания, от которого Ньютон должен был исходить.

В течение двух столетий, предшествующих деятельности Ньютона, передовые учёные занимались накапливанием опытных данных и аргументов для опровержения освящённой временем концепции, согласно которой в центре вселенной находится Земля, благосклонно освещаемая Солнцем, а Луна, планеты и звёзды являются живописной декорацией. Общепризнано, что Николай Коперник (Родился в Польше в 1473 г)) сделал больше всех, чтобы опровергнуть представление о неподвижной Земле - представление, которое долгое время поддерживалось последователями древнегреческого философа Аристотеля. На рис. 15 изображена принятая в древности схема движения планет, если смотреть с неподвижной Земли.

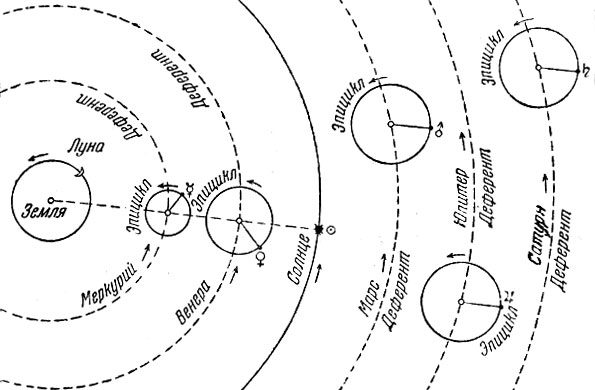
Рис. 15. Солнечная система по старинному представлению. Движения планет вокруг неподвижной Земли. Согласно древнегреческому астроному Птолемею, планеты двигались по небольшим кругам (эпициклам) вокруг 'фиктивных планет', которые в свою очередь двигались по большим кругам (деферентам) вокруг Земли

После того как концепция движущейся Земли была признана возможной, хотя ещё и не доказана окончательно, перед учёными встала последующая трудная задача - объяснить, как Земля движется и почему она движется. Звёзды, которые на самом деле представляют собой далёкие солнца, слишком удалены от нас, чтобы по их годовому смещению можно было обнаружить перемещение Земли относительно Солнца на 149 500 000 км в ту и в другую стороны; это смещение звёзд не удавалось обнаружить измерениями в течение длительного периода после изобретения телескопа. Можно вполне посочувствовать критикам новой теории, которые упорно утверждали, что Земля неподвижно покоится в пространстве, приводя следующий довод: "Если она движется, чему эти юные выскочки хотят заставить нас поверить, то почему же звёзды втечение года не совершают колебаний по небу вперёд и назад?" Это возражение является вполне здравым и было опровергнуто только за последнее столетие на основе самой совершенной техники наблюдений. Ближайшая к нам звезда, α Центавра, находится от нас на расстоянии 270 000 астрономических единиц. Если смотреть с этой звезды, то радиус орбиты Земли покажется меньше толщины человеческого волоса, находящегося на расстоянии пятнадцати метров от глаза. Таким образом годовое смещение звезды α Центавра выражается углом, меньшим чем видимое движение этого волоса, если его сместить на два его поперечника. Для всех остальных звёзд годовое смещение ещё меньше.

В то время как упомянутый аргумент против движения Земли был в полной силе, всё более трудной становилась задача предвычисления положений Солнца и планет с той точностью, какой требовала всё возрастающая точность наблюдений. Изобретение часов ещё острее выявило необходимость более точного предвычисления положений небесных тел и усовершенствования приборов для измерения направлений на небе. Необходимо было точно знать, как в действительности движутся планеты в пространстве.

Суточное вращение Земли (рис. 16) и её годовое обращение вокруг Солнца, как мы теперь знаем, невероятно усложняют проблему, так как все измерения должны быть сделаны на Земле, т. е. на теле, которое само находится в движении. Кроме того, лучи света должны пройти через атмосферу, которая вблизи горизонта может отклонить их до полуградуса.

Рис. 16. Земля вращается вокруг своей оси. Фотография области вокруг северного полюса неба. Получена с помощью неподвижной камеры, наведённой на северный полюс (восьмичасовая экспозиция). Полярная звезда дала толстую черту вблизи центра

Влияние вращения Земли и земной атмосферы можно в значительной степени устранить, если установить истинные положения звёзд в неподвижной системе, включающей в себя всё небо, и затем измерять положения планет относительно звёзд. На рис. 17 изображено видимое движение Марса во время одного из противостояний его с Солнцем. Эта странная кривая на фоне звёзд мало похожа на плавную кривую действительного движения Марса, изображённую на рис. 1.

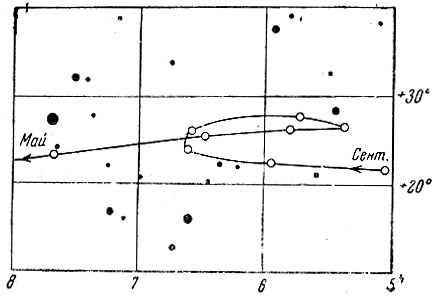
Рис. 17. Движение Марса среди звёзд. Показан путь, пройденный Марсом в течение четырёх месяцев. Кружки показывают его положения через каждые полмесяца

В XVI в. великий датский астроном Тихо Браге задумался над тем, что можно сделать, чтобы лучше изучить движение планет. Принцип его работы должен усвоить каждый учёный, так как в нём заключается самое существо правильно поставленного научного исследования. Тихо Браге произвёл много наблюдений со всей возможной точностью, доступной лучшим инструментам, которые он мог достать, а затем тщательно изучил свои инструменты с целью определения величины ожидаемых ошибок. Обширная серия наблюдений Марса, произведённых Тихо Браге, была затем самым тщательным образом обработана Иоганном Кеплером. Кеплер перепробовал для Марса все виды движения, которые он мог придумать. Некоторые типы эксцентрических движений Марса вокруг Солнца (Имеется в виду движение по круговым орбитам, центр которых не совпадает с Солнцем. (Прим. ред.))) удовлетворяли наблюдениям почти так же хорошо, как это требовалось, но Кеплер стремился к идеалу. Благодаря своей настойчивости он в конце концов пришел к открытию трёх весьма простых законов, описывающих движение планеты вокруг Солнца. Если какой-либо простой закон хорошо удовлетворяет наблюдениям, он почти всегда является правильным. Кеплер был уверен, что он добрался до истины в вопросе о планетных движениях, и время подтвердило его мнение.

Первый закон Кеплера гласит, что орбита планеты есть эллипс, в одном из фокусов которого находится Солнце. Эллипс представляет собой одну из простейших замкнутых плоских кривых; эта кривая всегда привлекала математиков, так как относительно неё может быть сформулировано множество простых теорем. Получить эллипс почти так же легко, как начертить круг. Для этого нужно только взять конус (прямой круглый конус) и пересечь его плоскостью. Кривая, по которой пересекаются конус и плоскость, и есть эллипс [см. сечение (а) на рис. 18]. Вы можете, конечно, проявить некоторую изобретательность и провести плоскость либо через вершину конуса - тогда в пересечении вы получите только одну точку, либо перпендикулярно к оси конуса - тогда в пересечении получится окружность [сечение (b) на рис. 18], либо же параллельно образующей конуса. В этом последнем случае эллипс не замыкается, превращаясь в параболу [сечение (с)] или даже в гиперболу [сечение (d)], если плоскость близка к вертикали. Математик называет все такие кривые коничесуими сечениями и формулирует относительно них ряд общих теорем.

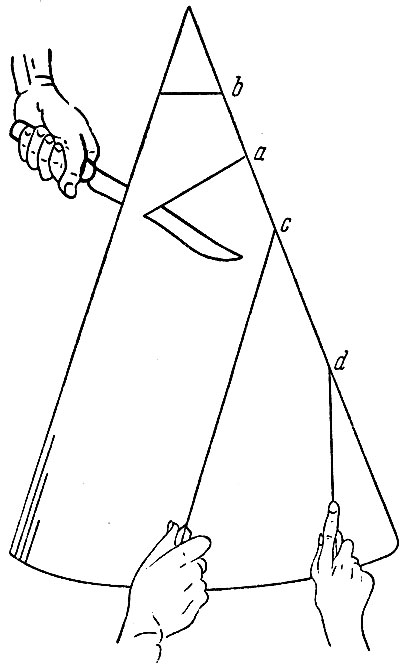
Рис. 18. Сечения конуса плоскостью. В сечении образуются: (а) эллипс, (b) окружность, (с) парабола или (d) гипербола. Эти плоские кривые называются коническими сечениями

Найти фокус эллипса немногим сложнее, чем получить эллипс в сечении конуса. Если мы проведём прямую из одного фокуса и затем начертим её отражение от эллипса под таким же углом к касательной, то это отражение обязательно пройдёт через второй фокус эллипса, как показано на рис. 19. Для параболы задача ещё упрощается, так как в этом случае все лучи, исходящие из фокуса, отражаются, как пучок параллельных прямых. В этом заключается принцип действия прожекторов и автомобильных фар. Наоборот, устройство отражательного телескопа основано на том, что параллельные световые лучи от далёкой звезды при отражении от поверхности параболического зеркала собираются в одну точку в фокусе (рис. 20).

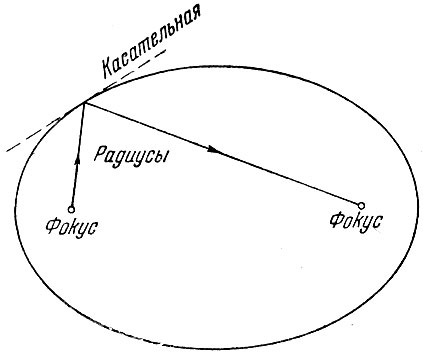
Рис. 19. Эллипс. Радиусы, проведённые из двух фокусов, образуют одинаковые углы с касательной. Эксцентриситет этого эллипса равен 0,72

Другое замечательное свойство эллипса состоит в том, что для любой его точки сумма расстояний до двух фокусов есть величина постоянная. На этом свойстве основан весьма лёгкий способ черчения эллипса. Воткните в лист бумаги две крепкие булавки в те точки, где должны быть фокусы. Затем наденьте на эти булавки петлю из какой-либо нерастяжимой нити, туго натяните петлю карандашом и чертите эллипс, обводя карандашом с внутренней стороны туго натянутой петли (рис. 21). Если обе булавки сблизить так, чтобы они оказались совсем рядом, мы получим окружность - простейший эллипс.

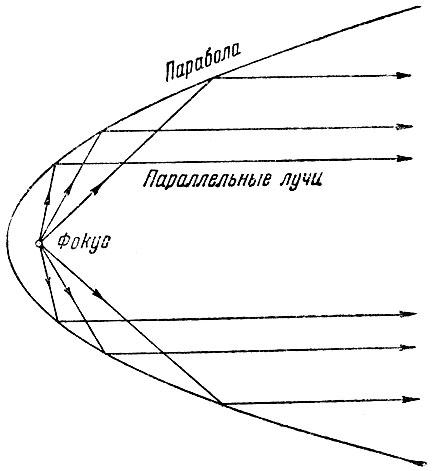
Рис. 20. Парабола. Все радиусы, исходящие из фокуса, отражаются параболой в виде параллельных прямых

Согласно первому закону Кеплера, Солнце всегда находится в одном фокусе эллипса, а другой фокус пустует. На рис. 22 представлены различные возможные орбиты. Ближайшая к Солнцу точка орбиты называется перигелием, а наиболее удалённая - афелием. Среднее расстояние равно полусумме расстояний в перигелии и в афелии или половине большей оси эллипса. Форма орбиты определяется эксцентриситетом, т. е. отношением разности расстояний перигелия и афелия к их сумме. Для окружности эксцентриситет равен нулю, для параболы - 1,0, а для полей мужской шляпы примерно - 0,5.

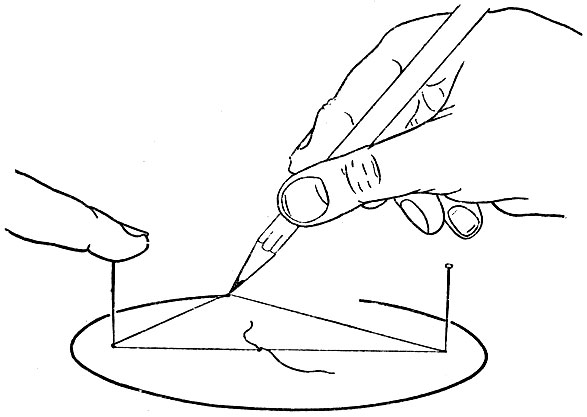
Рис. 21. Черчение эллипса. Эллипс можно легко начертить с помощью двух булавок и нитяной петли

Орбита Земли представляет собой почти окружность, эксцентриситет её равен всего 1/60, На глаз такой эллипс кажется хорошо начерченным кругом, но фокус явно находится не в центре. Меркурий и Плутон являются, единственными планетами, орбиты которых сильно отклоняются от окружности; эксцентриситеты их равны соответственно 0,21 и 0,25. Таким образом расстояние Плутона от Солнца изменяется от 30 астрономических единиц в перигелии (меньше среднего расстояния Нептуна) до 50 астрономических единиц в афелии. Легко проверить эти данные, если учесть, что среднее из 30 и 50 есть 40 (т. е. среднее расстояние Плутона в астрономических единицах) и что разделив (50-30) на (50+30) мы получим 20/80, т. е. эксцентриситет, равный 0,25.

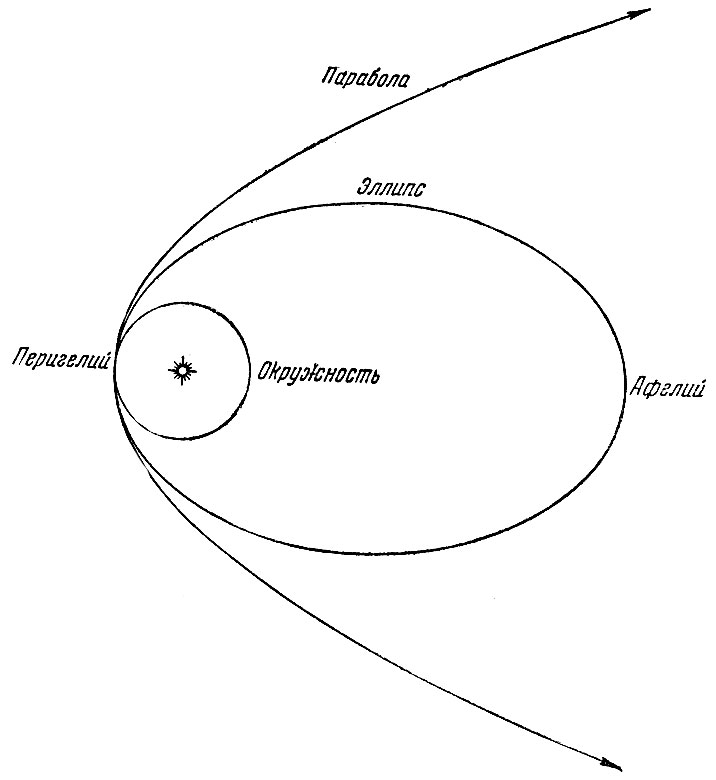
Рис. 22. Различные орбиты. Кометы движутся по очень вытянутым эллиптическим орбитам, почти совпадающим с параболами вблизи Солнца. Планеты движутся по эллиптическим орбитам с малым эксцентриситетом

Второй закон движения планет, сформулированный Кеплером, проще первого закона. Он гласит что прямая, соединяющая планету с Солнцем, в равные промежутки времени описывает равные площади. Согласно этому закону, когда планета находится близко от Солнца, в перигелии, она должна двигаться с большей скоростью чем когда она далеко от Солнца, например в афелии, как изображено на рис. 23. Скорость Плутона равна 6,1 км/сек в перигелии и 3,7 км/сек в афелии. Отношение этих скоростей равно 5/3, как можно было догадаться, судя по отношению расстояний. В перигелии (около 1 января) скорость Земли увеличивается на 0,9 км/сек по сравнению с её скоростью в афелии, равной 29,1 км/сек.

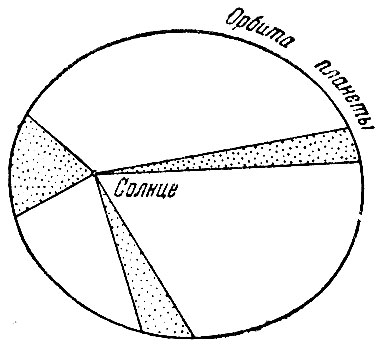
Рис. 23. Равные площади описываются в равные промежутки времени. Заштрихованные площади равны. Эксцентриситет эллипса равен 0,5

Третий закон Кеплера гласит, что квадраты периодов обращения планет вокруг Солнца относятся как кубы их средних расстояний от Солнца. Этот закон даёт лёгкий способ вычисления периода обращения, если нам известно среднее расстояние тела, обращающегося вокруг Солнца. Выразим среднее расстояние в астрономических единицах. Возведём это расстояние в куб. Квадратный корень из куба расстояния даёт нам период обращения в годах. Для Земли эта формула удовлетворяется; квадратный корень из 1³ есть 1; период обращения Земли равен одному году. Для Нептуна среднее расстояние равно 30 астрономическим единицам; 30³ = 27 000; корень квадратный из 27 000 есть 164, т. е. период обращения Нептуна в годах. Мы получим более точное значение периода - 164,8 лет, если воспользуемся более точным значением среднего расстояния.

С помощью трёх законов Кеплера мы можем предсказывать движения планет на долгие годы вперёд. Теперь при этом вводят лишь две поправки. Первая поправка вводится вследствие того, что каждая планета оказывает возмущающеэ действие на движение других планет; вторая, весьма небольшая, поправка должна быть сделана для орбиты Меркурия, чтобы учесть эффект, предсказанный теорией относительности Эйнштейна.

Ньютон был прекрасно знаком с законами Кеплера, описывающими движение планет, а также с революционной идеей Галилея (Галилео Галилей родился в Пизе, Италия, в 1564 г)) о том, что все тела падают с одинаковой скоростью, независимо от их размера. Галилей доказывал своё положение, бросая большие и маленькие пушечные ядра с Падающей Башни в Пизе, однако, почти никого не убедив, сам подвергся гонениям со стороны церкви за высказывание взглядов, противоречащих религии. Галилей высказывал и другие, не менее "возмутительные", идеи, например, что движущееся тело останавливается только потому, что его движение задерживается трением, а не потому, что пространство обладает каким-то внутренне присущим ему свойством останавливать все движущиеся тела.

Ньютон развил идеи Галилея относительно движения материальных тел в пустом пространстве и сформулировал их в виде трёх простых законов. Эти принципы движения теперь всем настолько хорошо знакомы, что мы приводим их только для полноты. Первый принцип гласит, что тело остаётся в покое или сохраняет своё состояние равномерного прямолинейного движения до тех пор, пока какая-либо сила не выведет его из этого состояния) второй принцип утверждает, что величина ускорения пропорциональна действующей силе и обратно пропорциональна массе тела; наконец, согласно третьему принципу, сила действия и сила прсйпиводействия равны и противоположны по направлению.

Совершенно очевидное приложение этих законов встречается всюду, в особенности в нашем современном мире механизмов. Непонимание природы сил трения как в воздухе, так и между движущимися частями механизмов было единственным препятствием, в силу которого эти законы не были открыты гораздо раньше.

Установив свои принципы движения, Ньютон начал размышлять над проблемами движения Луны и планет. Поскольку Земля притягивает яблоко, пушечное ядро и перышко с силой, пропорциональной их массам, то почему бы ей не притягивать также и Луну? Луна по всем правилам должна была бы двигаться по прямой линии до тех пор, пока на неё не подействовала бы какая-нибудь сила, но на самом деле Луна движется вокруг Земли по криволинейной орбите. Таким образом Луна постоянно падает к Земле, причём скорость этого падения измеряется отклонением движения Луны от прямолинейного (рис. 24). Отсюда можно заключить, что притяжение Земли действует на Луну с силой, величина которой такова, что она как раз вызывает наблюдаемое падение Луны. Другими словами, сила притяжения Земли должна в точности уравновешивать центробежную силу Луны, развивающуюся при её обращении вокруг Земли. Ньютон нашёл, что если бы сила притяжения изменялась обратно пропорционально квадрату расстояния от центра Земли, то на расстоянии Луны она имела бы как раз требуемое значение (Говорят, что Ньютон на много лет задержал опубликование закона всемирного тяготения вследствие трудности доказательства того факта, что Земля притягивает так, как если бы вся её масса была сосредоточена в центре)).

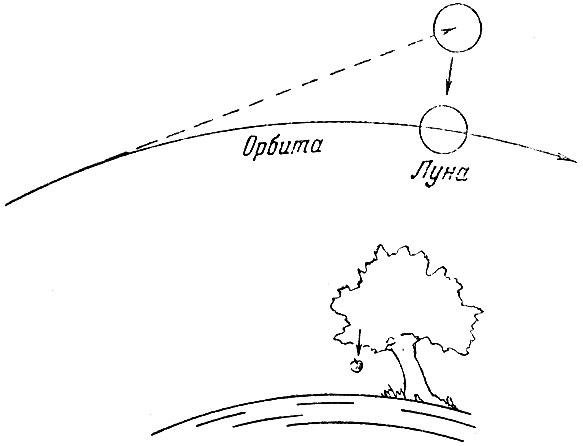
Рис. 24. Падающая Луна и падающее яблоко. Ньютон пришёл к убеждению, что притяжение Земли заставляет Луну падать, уклоняясь от прямолинейного движения; падение Луны и падение яблока с дерева совершается по одному и тому же закону

Исходя из законов Кеплера, Ньютон смог также доказать математически, что планеты притягиваются к Солнцу той же самой силой. Сопоставляя все полученные им результаты, Ньютон пришёл к выводу, что всякая частица материи во вселенной притягивает всякую другую частицу с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними. Этот закон всемирного тяготения обьясняет все сложнейшие движения в солнечной системе с максимальной степенью точности, достижимой в астрокомических измерениях (до одной миллионной). Единственным исключением является поступательное движение перигелия Меркурия примерно на 50 секунд в столетие; это движение объясняется небольшой поправкой к закону Ньютона, необходимость которой была предсказана теорией относительности Эйнштейна. (Под углом 50 секунд нам будет видна радужная оболочка глаза, если смотреть с расстояния 50 м.)

Таким образом солнечная система не распадается благодаря притяжению, которое Солнце оказывает на планеты, а системы спутников - благодаря притяжению планет. Проблема была бы весьма проста и полностью решалась бы законами Кеплера, если бы не несчастное обстоятельство, что все планеты притягивают друг друга, также как своих спутников и Солнце. Это всеобщее притяжение настолько усложняет проблему, что не существует её точного математического решения. Единственное облегчение состоит в том, что массы планет гораздо меньше массы Солнца, так что силы взаимодействия между планетами, пропорциональные их массам, гораздо меньше, чем сила притяжения Солнца. Точно так же массы спутников гораздо меньше масс их планет. Поэтому законы движения Кеплера могут дать приближённое решение задачи о движении, а чтобы учесть силы взаимного притяжения планет, следует вводить небольшие поправки. Эти небольшие поправки носят название возмущений, так как движение исследуемой планеты возмущается прочими планетами.

Наиболее сложную задачу о возмущениях представляет движение системы Земля -Луна; здесь Солнце возмущает движение Луны вокруг Земли. Строго говоря, Земля возмущает движение Луны вокруг Солнца, так как Солнце естественно притягивает Луну примерно вдвое сильнее, чем Земля. Несмотря на это, нет никакой опасности, что Солнце "украдёт" Луну у Земли и оставит нас без вдохновения тёплых летних ночей. Система настолько компактна, Луна и Земля движутся настолько близко друг к другу, что притяжение Солнца лишь заставляет оба тела обращаться вокруг него по орбите, которая в среднем является эллиптической. Основные результаты сводятся к следующему: во-первых, орбита Луны никогда не является выпуклой по направлению к Солнцу (рис. 25) и, во-вторых, астрономы должны ещё много поработать для предвычисления движения Луны. Уравнение точного движения Луны занимает около 250 страниц большого формата.

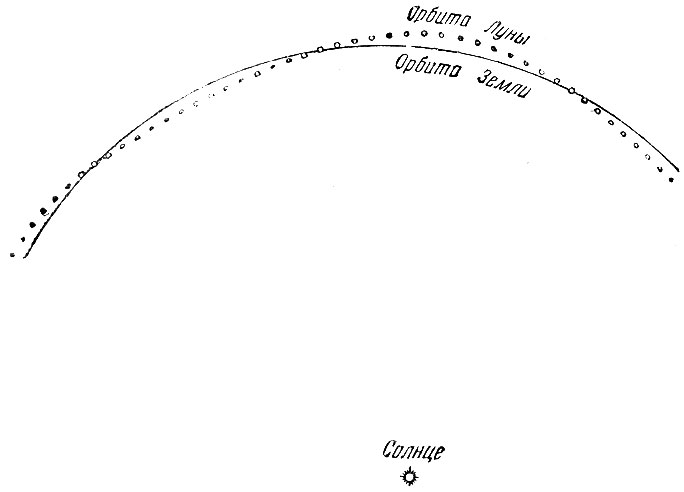
Рис. 25. Орбита Луны вокруг Солнца. Отклонения от идеального эллипса сильно преувеличены на чертеже; даже при этом видно, что орбита Луны всегда вогнута по направлению к Солнцу, в чём можно убедиться, наклонив страницу и смотря вдоль ряда кружков

Юпитер безусловно является самым своевольным ребёнком в солнечной семье, так как он возмущает движение всех планет и астероидов. Обладая массой, равной 1/1000 массы Солнца, т. е. "львиной долей" массы всей семьи планет, Юпитер производит возмущения гораздо большие, чем все прочие планеты, в особенности среди астероидов, которые подходят к нему ближе, чем к другим планетам (рис. 7). Если вычислить орбиту астероида без учёта притяжения Юпитера, то ошибки за несколько лет могут достичь многих градусов. Таким образом астероиды иногда "теряются", а затем снова открываются и отождествляются по орбитам и блеску. Периоды обращения астероидов не могут находиться в простых отношениях (например 1/2 или l/3) к периоду Юпитера. Причину этого легко понять. Возьмём случай, когда три обращения астероида совершаются в точности за тот же промежуток времени, что и два обращения Юпитера. Возмущения, накопившиеся за время трёх обращений астероида, удвоятся за время трёх следующих обращений и так дальше, вследствие чего орбита существенно изменится. Этот процесс можно сравнить с движением автомобиля по неровной дороге, с рядом рытвин, расположенных на равных расстояниях одна от другой. Если скорость такова, что период собственных колебаний рессор автомобиля равен времени его прохождения между двумя рытвинами, то колебания усиливаются при каждой встряске, пока рессора не лопнет или пока водитель не переведёт машину на другую скорость. Астероиды также принуждены менять свои скорости, когда они близки к критическим значениям. В результате на кривой, представляющей количество астероидов, распределённых по их периодам, имеются явные пробелы (Известные под названием пробелов Кирквуда; они были названы так в честь открывшего их астронома, жившего в XIX в)) в тех местах, где должны находиться астероиды, периоды которых кратны периоду Юпитера (рис. 26).

Рис. 26. Пробелы Кирквуда. Вверху пробелы в средних расстояниях астероидов, внизу - деления колец Сатурна. Обратите внимание на широкие промежутки для отношений периодов 1/2 и 1/3

В кольцах Сатурна, относительно которых мы уже говорили, что они "аналогичны системе астероидов, наблюдается точно такое же явление. Тот факт, что мы имеем кольца, а не одно единственное кольцо, является результатом возмущений мелких астероидов в кольцах со стороны трёх внутренних спутников: Мимаса, Энцелада. и Фетиды. Эти спутники принуждают малые частицы в кольцах избегать некоторых определённых скоростей в их движении вокруг Сатурна, в результате чего на критических расстояниях мы наблюдаем тёмные полосы. Деление Кассини, ясно заметное тёмное пространство между внешним и средним кольцами на рис. 27, занимает область, в которой крошечные астероиды могли бы двигаться с периодами, равными 1/2 периода Мимаса, 1/3 периода Энцелада и 1/4 периода Фетиды, т. е. с периодом несколько большим И часов. Другие теоретически вычисленные "тёмные кольца" также могут наблюдаться.

Рис. 27. Сложные кольца Сатурна. С рисунка, сделанного на основе визуальных наблюдений. На верхнем рисунке кольца видны почти в ребро. Тень от них заметна на диске. Пять делений колец можно видеть лишь при самых лучших условиях наблюдения

Отмеченный нами ранее факт, что масса Солнца огромна по сравнению с массами планет, а массы планет в свою очередь огромны по сравнению с массами спутников, не является просто счастливой случайностью, служащей для удобства астрономов. Весьма сомнительно, чтобы солнечная система могла долго существовать, если бы массы планет были сравнимы с массой Солнца. Ни одно из тел не могло бы оставаться вблизи центра тяжести, как Солнце в солнечной системе, но все они двигались бы по сложным кривым, форму которых почти нельзя было бы предугадать. Хотя математики не могут дать полного решения даже задачи о движении трёх тел примерно одинаковой массы, но всё же рассмотрение этой сравнительно простой задачи показывает, что в нашем сложном случае мы получим катастрофические результаты. Одни планеты уничтожились бы в результате столкновений, другие были бы выброшены из системы, и в конце концов в системе, по всей вероятности, остались бы два самых больших тела, обращающихся друг относительно друга на сравнительно небольшом расстоянии, причём каждое из них имело бы небольшого спутника или даже систему спутников. Несколько других небольших тел могло бы остаться в системе на весьма далёких расстояниях от двух больших тел. Наблюдения двойных и кратных звёзд показывают, что звёзды обнаруживают тенденцию двигаться попарно, будучи разделены сравнительно большими расстояниями от других пар той же системы. Некоторые астрономы считают, что астероиды могут представлять собой остатки планеты, возможно как раз той планеты, которая пыталась конкурировать с Юпитером.

В настоящее время можно не опасаться, что солнечная система потеряет какие-либо планеты или что -произойдёт какое-либо крупное столкновение. Эта наша абсолютная уверенность в том, что катастрофы невозможны, распространяется на интервал времени в сотни миллионов лет. А мысль о возможности катастрофы по истечении этого промежутка времени не очень волнует нас в настоящий момент.