
Глава 5. Заполнение белых пятен - II. 1957-1972.
Койпер (1956) отметил, что предположение о формировании Плутона как протопланеты из первичной солнечной туманности несовместимо с его современными орбитальными характеристиками - большими эксцентриситетом и наклоном. Он исключил возможность того, что орбита Плутона могла быть впоследствии возмущена проходящей мимо звездой, указав на малую вероятность такого события и на то обстоятельство, что почти круговая орбита Нептуна, видимо, не подвергалась сильным возмущениям. Вместо этого он предположил, что Плутон первоначально образовался как спутник прото-Нептуна. Гипотеза Койпера отличается от гипотезы Литлтона (1936), согласно которой Плутон и Тритон первоначально оба были спутниками Нептуна до их тесного сближения, в результате которого движение Тритона стало обратным, а Плутон был выброшен из системы. Койпер считал, что Плутон мог сохранить большой период вращения, как следствие своего происхождения в качестве спутника Нептуна. Фотометрические наблюдения Плутона, начавшиеся в 1952 г. и достигшие высшей точки в работе Уокера и Харди (1955), установили значение периода вращения 6,4 сут.
Рабе (1954) использовал результаты ограниченной задачи трех тел, и в частности интеграл Якоби (9)
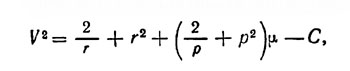
где r и р - расстояния спутника от Солнца и от планеты соответственно в единицах расстояния между Солнцем и планетой, С -постоянная Якоби, μ - масса планеты, а V - скорость спутника во вращающейся системе координат ограниченной задачи трех тел.
По предложению Койпера Рабе (1957 а) добавил переменные массы прото-Юпитера и прото-Сатурна к солнечной массе М для изучения эволюции орбиты Плутона при совместном уменьшении масс Нептуна, Юпитера и Сатурна. Включение двух переменных масс М и μ означает, что уравнение (9) должно быть переписано в виде (1)

где r и р - расстояние спутника от М и μ соответственно, V - его линейная скорость во вращающейся системе координат, а С - переменная Якоби.
Из уравнения (1) следует, что совместное уменьшение масс dM и dμ приведет к следующему изменению С: (2)
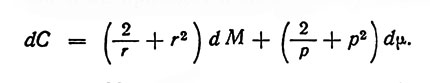
Здесь dM и dμ отрицательны при убывающих массах, и, следовательно, С будет уменьшаться. Если движение спутника не происходит в плоскости движения масс М и μ, то должен быть учтен член для координаты z: (3)
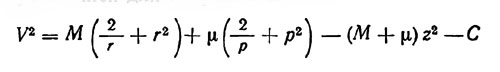
и уравнение (2) приобретает тогда следующую форму: (4)
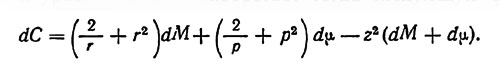
Рабе (1957 а) использовал уравнение (3) и значения r, z и V, данные Эккертом, Брауэром и Клеменсом (1951) для того, чтобы вычислить С на произвольную дату - июль 10,0, 1921. Полученный результат С=2,901 и современная орбита Плутона согласуются с предположением Койпера (1956) о происхождении Плутона в системе прото-Нептуна при условии, что общая потеря массы протопланет dM после выбрасывания Плутона из системы Нептуна составляла 0,04 массы Солнца. По оценкам Койпера (1957), масса самого Нептуна уменьшилась за счет испарения под влиянием Солнца в 40 раз до выброса Плутона.
Рабе (1957b) заметил, что, хотя вышеприведенные результаты вполне удовлетворительны, из них не следует, что начальное среднее движение Плутона как планеты было столь же близким к соизмеримости 2:3 со средним движением Нептуна, как в наше время. Он предположил, что дальнейшая орбитальная эволюция после выброса из системы прото-Нептуна привела к постепенному достижению современной близкой соизмеримости. Вышеупомянутая потеря масс протопланет dM, происшедшая после выброса Плутона, вызвала увеличение угла эксцентриситета φ от 11° до современного значения 14,4°, а также увеличение наклона i по сравнению с его неизвестным начальным значением.
Гипотеза Койпера (1956) о спутнике прото-Нептуна, подкрепленная вычислениями Рабе (1957 а, b), должна была реализовываться на более ранней стадии развития Солнечной системы, чем гипотеза Литлтона (1936) взаимодействия пары Тритон- Плутон. Голдрайх и Сотер (1966) предположили, что до своего взаимодействия и Плутон, и Тритон имели орбиты с прямым движением, лежащие в экваториальной плоскости Нептуна или вблизи нее, причем неодинаковая приливная эволюция в конце концов привела их к тесному сближению. В случае если масса Плутона не слишком превосходит массу Тритона, такое сближение могло при сохранении момента количества движения изменить направление движения Тритона и выбросить Плутон, придав орбитам обоих тел значительные эксцентриситеты и наклоны. Голдрайх и Сотер указали, что гипотеза Литлтона поддерживается найденным Уокером и Харди (1955) значением 6,39 сут для периода вращения Плутона. Действительно, если период синхронного обращения Плутона вокруг Нептуна когда-то имел такое значение, то Плутон должен был находиться за пределами современной орбиты Тритона, который имеет период 5,88 сут. Приливы, вызываемые Тритоном на Нептуне и в особенности приливы, вызываемые Нептуном на Тритоне, должны были затем в течение ~1017 с (≈ 3*109 лет) погасить значительный эксцентриситет орбиты Тритона, появившийся в результате тесного сближения с Плутоном.
Голдрайх и Сотер отметили, что подобный приливной механизм мог бы уменьшить эксцентриситет Тритона и в случае его захвата на обратную орбиту. Они также указали, что повышающаяся таким образом вероятность гипотезы Литлтона делает правдоподобным менее аномальное значение плотности Плутона, чем значение ~50 г/см3, требуемое для того, чтобы планета диаметром, соответствующим данным Койпера, могла вызвать возмущения в движении Урана и Нептуна. Они предполагают, что возмущения могут быть приписаны транснептуновому поясу комет, существование которого было постулировано Уипплом (1964). Если, как требуется гипотезой Литлтона, масса Плутона не намного больше массы Тритона, скажем, не более чем вдвое, то плотность Плутона станет меньше ~2,3 г/см3, что согласуется со значениями, найденными для спутников больших планет.
Мак-Корд (1966) детально исследовал динамическую эволюцию системы спутников Нептуна и подтвердил, что механизм приливного трения мог привести даже очень эксцентричную орбиту Тритона к ее современному виду за время существования Солнечной системы. По его мнению, Тритон будет быстро приближаться к Нептуну, в течение 10-100 миллионов лет достигнет предела Роша и разрушится. Мак-Корд считает происхождение Тритона путем захвата вполне возможным, но также не исключает и гипотезы столкновения Тритон - Плутон.
Коэн и Хаббард (1964, 1965) исследовали эволюцию орбиты Плутона путем численного интегрирования уравнений движения пяти внешних планет на интервале более чем 120 000 лет назад от нашей эпохи, Вычисления производились на машине NORC в Лаборатории ВМС США со скоростью ~1500 лет за час машинного времени. При этом использовались данные Эккерта, Брауэра и Клеменса (1951). Программа давала геометрические характеристики каждого относительного минимума расстояния между Плутоном и Нептуном.
Первое тесное сближение АА' пришлось на календарную дату август 27, 1896, когда средняя аномалия Плутона составляла 210° и Плутон отставал от Нептуна на 6° по истинной долготе, а расстояние между ними было 19 а. е. В течение одного синодического периода, равного примерно 500 лет, когда Плутон совершает 2 оборота, а Нептун - 3, имеют место два других относительных минимума ВВ' и СС, при которых взаимные расстояния составляют 25 и 52 а. е. соответственно. Эти минимумы наступают, когда Плутон находится вблизи перигелия. При последовательных синодических периодах координаты Плутона и Нептуна испытывают либрацию с периодом ~ 19670 лет, как это очевидно из графика изменения расстояния при тесном сближении АА' или из графика значений истинной аномалии Плутона в момент наиболее тесного сближения. Последний график изображен на рис. 5.1 (Коэн, Хаббард, 1965).
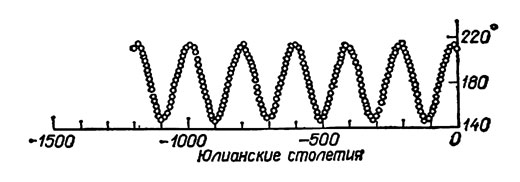
Рис. 5.1. Истинная аномалия Плутона при тесном сближении АА' (Коэн, Хаббард, 1965)
На рис. 5.2 (Коэн, Хаббард, 1965) показана картина положений и движений при тесных сближениях. Орбиты здесь даны в проекциях на неизменную плоскость. Верхний ряд на этом рисунке охватывает синодический период, когда либрация положений при тесном сближении достигает своего первого экстремума приблизительно 1500 лет назад от нашей эпохи. Здесь показано положение Плутона и Нептуна при последовательных тесных сближениях АА', ВВ' и СС на протяжении этого синодического периода. Второй ряд показывает положения при сближениях АА', ВВ' и СС в течение синодического периода на 5000 лет раньше, а положения третьего ряда отстоят еще на 5000 лет назад. Все три ряда охватывают половину периода либрации; до этого интервала времени и после него движение происходит в обратном порядке и периодически повторяется.
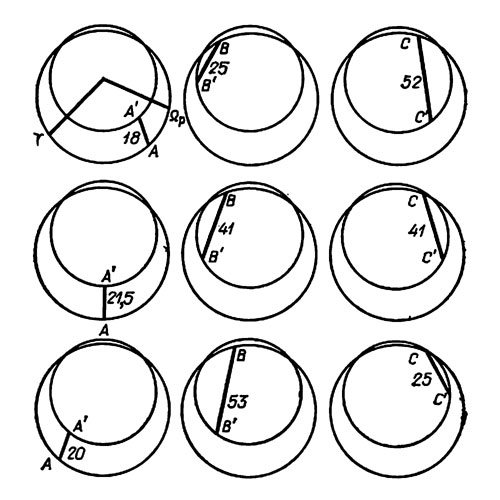
Рис. 5.2. Либрация тесных сближений; расстояния даны в а. е. (Коэн, Хаббард, 1965)
Либрация при тесных сближениях может быть выражена в классических переменных путем представления угла отклонения фаз Плутона и Нептуна от соизмеримости в виде
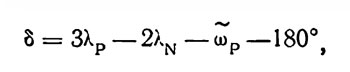
где λ - средняя долгота, ω - долгота перигелия, а Р и N - индексы для Плутона и Нептуна соответственно. Угол δ осциллирует относительно среднего значения 180° с амплитудой 76° и с периодом 19670 лет.
Помимо средней аномалии, другие элементы орбиты Плутона также подвержены изменениям. Большая полуось а испытывает изменения с периодом 19670 лет и амплитудой 0,14 а. е. Эксцентриситет е обнаруживает уменьшение на 0,005 в 120000 лет с периодом не менее 1 млн. лет. Наклон i возрастает примерно на 0,2° в 120000 лет и также имеет период не менее 1 млн. лет. Узел отступает по орбите приблизительно на 9,5° в 100000 лет, что дает период 4 млн. лет. Аргумент перигелия, имевший в начальную эпоху значение 113,6°, возрастает со скоростью 1,2° за 100000 лет, совершая полный оборот по орбите за 30 млн. лет.
Механизм либрации может быть наглядно представлен с помощью рис. 5.3. Коэн, Хаббард и Остервинтер (1979) дают следующее объяснение:
"Траектория Плутона изображается в гелиоцентрической системе координат, вращающейся с угловой скоростью Нептуна. Орбита Плутона нарисована для синодического периода, а две петли соответствуют двум последовательным прохождениям Плутона через перигелий. В течение периода либрации, составляющего 80 оборотов Плутона, синодическая траектория испытывает вращательные колебания вокруг точки S относительно линии Солнце-Нептун. Вместо изображения либрации траектории при фиксированном положении Нептуна N рисунок показывает движение Нептуна N - N относительно синодической траектории. Заметим, что направление движения относительно вращающейся системы, как показано на рисунке, противоположно направлению относительно невращающейся инерциальной системы. Рассмотрим направление и величину возмущающего ускорения, обусловленного действием Нептуна на Плутон, соединяя положения Нептуна и Плутона, когда Нептун находится в экстремальных точках либрации. Чтобы выделить компоненту этой силы, оказывающую главное влияние на движение Плутона, возьмем компоненту, которая перпендикулярна линии Солнце-Плутон. Среднее по времени от этой компоненты, взятое вдоль синодической траектории, как легко видеть, будет в основном определяться компонентой, соответствующей положению Плутона в ближайшей к Нептуну петле перигелия. Таким образом, ясно, что тангенциальная компонента силы в среднем ускоряет Плутон в направлении его движения в инерциальной системе, когда Нептун находится в левой половине дуги N - N (рис. 5.3), и в направлении, противоположном его движению, когда Нептун находится в правой половине этой дуги. На основе соображений, касающихся энергии и периода, очевидно, что Нептун ускоряется вправо, когда он находится в левой половине дуги относительно синодической траектории, и ускоряется влево, когда находится с правой стороны. Этот процесс можно сравнить с движением маятника, поскольку Нептун движется вперед и назад по дуге N - N. Сила, которая вызывает это либрационное движение Нептуна, может быть интерпретирована как взаимное отталкивание между Нептуном и петлями перигелия Плутона".
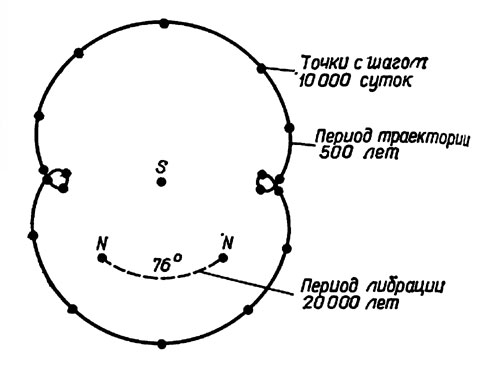
Рис. 5.3. Траектория Плутона в синодической системе Солнце - Нептун в граничных точках либрации (Коэн, Хаббард, 1965)
В силу либрации около отношения соизмеримости минимальное расстояние сближения Плутона с Нептуном составляет около 18 а. е. и достигается вблизи афелия. Поэтому очень тесное сближение, которое могло бы произойти вблизи перигелия и сильно возмутить орбиты планет, совершенно исключается. Это серьезно ослабляет гипотезу, что Плутон был когда-то связан с системой спутников Нептуна.
Коэн и Хаббард (1965) использовали данные об орбите Плутона, опубликованные Эккертом, Брауэром и Клеменсом (1951), которые в свою очередь основывались на элементах Плутона, полученных Бауэром (1931). В 1967 г. Коэн, Хаббард и Остервинтер повторили работу 1965 г., расширив протяженность исследуемого интервала до 300000 лет и использовав улучшенные элементы орбиты Плутона при сохранении значений 1951 г. для остальных планет. Орбита Плутона была улучшена по методу наименьших квадратов с использованием наблюдений, сделанных между 1914 и 1965 гг. Некоторые из этих наблюдений ранее не публиковались.
Из работы Шараф (1955) были взяты результаты 14 наблюдений до открытия, а из работы Шараф и Будниковой (1964) - 33 нормальных места в интервале 1930-1958 гг. Всего было использовано 183 наблюдения, полученных с помощью 60-сантиметрового Йеркского и 215-сантиметрового Мак-Дональдского рефлекторов. Кроме того, использовалось более 300 наблюдений, сделанных главным образом Лампландом на 105-сантиметровом рефлекторе Ловелловской обсерватории. Данные 21 наблюдения Йеркской обсерватории, опубликованных ван Бисбруком (1963) и 9 наблюдений, использованных Холидеем и сотрудниками (1966) в их работе по покрытиям, дополняли наблюдательный материал. Для получения весов различных групп наблюдений использовались четыре отдельных решения, по одному на каждую группу данных - отдельно для данных Шараф - Будниковой, обсерваторий Йеркс - Мак-Дональд, Ловелловской обсерватории, и, наконец, для данных Холидея.
Орбита Плутона, а также орбиты Юпитера, Сатурна, Урана и Нептуна были рассчитаны с помощью численного интегрирования. Новые элементы, полученные для Плутона, существенно отличаются от элементов Эккерта, Брауэра и Клеменса (1951), что и неудивительно. В табл. 10 (Коэн, Хаббард, Остервинтер, 1967) сравнены две системы элементов.

Таблица 10. Старые и новые элементы орбиты Плутона (Коэн, Хаббард, Остервинтер, 1967)
Коэн, Хаббард и Остервинтер (1967) уточнили параметры либрации, получив значение периода 19440 лет и значение амплитуды 80°. В 1971 г. они распространили свой интервал интегрирования до 1000000 лет.
Вильямс и Бенсон (1971) проинтегрировали уравнения движения Плутона на интервале 2,1 млн. лет вперед и 2,4 млн. лет назад. Для начала интегрирования они использовали элементы Коэна и коллег (1967). При интегрировании уравнений движения Плутона они сделали несколько упрощающих предположений. Влияние четырех внутренних планет учитывалось приближенно путем присоединения их масс к массе Солнца. Значение, использованное для величины обратной массе Плутона, составляло 1812 000 в единицах массы Солнца (Данком, Клепчинский и Сейделмен, 1968а, b). В табл. 11 (Вильямс, Бенсон, 1971) даны принятые значения масс внешних планет.

Таблица 11. Обратные значения масс внешних планет (Вильямс, Бенсон, 1971)
Вильямс и Бенсон подтвердили и уточнили значение периода либрации, равное 19951 лет, на интервале интегрирования в 4,5 млн. лет. Они нашли, что либрация совершенно устойчива и возможны лишь изменения ее среднего значения, приводящие к увеличению минимального расстояния сближения с Нептуном и повышающие тем самым устойчивость системы. В предположении, что эта устойчивость на промежутке интегрирования соответствует устойчивости на протяжении всего возраста Солнечной системы, можно заключить, что либрация Нептун - Плутон возникла еще в период формирования Солнечной системы. Авторы считают, что, прежде чем предпринимать интегрирование уравнений движения Плутона на еще более длительном интервале, желательно уточнить модель Солнечной системы.
Трудности, с которыми встретились Фиксмиллнер, Деламбр и Бувар (см. гл. 1) в попытках вычислить орбиту Урана, которая удовлетворяла бы как старым, так и новым наблюдениям, по-видимому, встают и перед современными исследователями, пытающимися найти решение для орбиты Нептуна. Данком, Клепчинский и Сейделмен (1968а, b) указывают на очевидную неспособность как прошлых, так и современных теорий движения Нептуна представить другие наблюдения, помимо тех, которые были первоначально использованы при построении данной теории. Например, теория Ньюкома (1899), которая была в хорошем согласии с наблюдениями 1795 и 1846-1896 гг., оказалась не в состоянии представить наблюдения в долготе с точностью лучшей 5" к 1938 г. даже при дополнительном учете возмущений от Плутона. Теория движения Нептуна, разработанная Эккертом, Брауэром и Клеменсом (1951), которая учитывала влияние Плутона с обратным значением его массы 360 000 и удовлетворяла наблюдениям 1795 и 1846-1938 гг., привела к отклонениям в наблюдаемой долготе Нептуна примерно в 4" к 1960 г.
Данком и его коллеги (1968 а, b) предположили, что эти неудачи указывают на необходимость другого значения массы Плутона. Они выполнили численное интегрирование уравнений движения пяти внешних планет для четырех разных значений обратной массы Плутона: 360000, 930000, 1500000, 2640000. Наилучшим должно было считаться то значение массы Плутона, при котором решение, построенное по наблюдениям 1846-1938 гг., лучше всего представляет наблюдения долготы на период 1960-1968 гг. Подобно Бувару (1821), отбросившему в свое время данные ранних наблюдений Урана (см. гл. 1), Данком и его коллеги опустили в своих вычислениях результаты наблюдений 1795 г., обосновывая свое решение во многом теми же причинами, что и Бувар.
На рис. 5.4 показаны невязки О-С в долготе орбиты λ и широте β по теории Эккерта, Брауэра и Клеменса с обратным значением массы Плутона 360000.
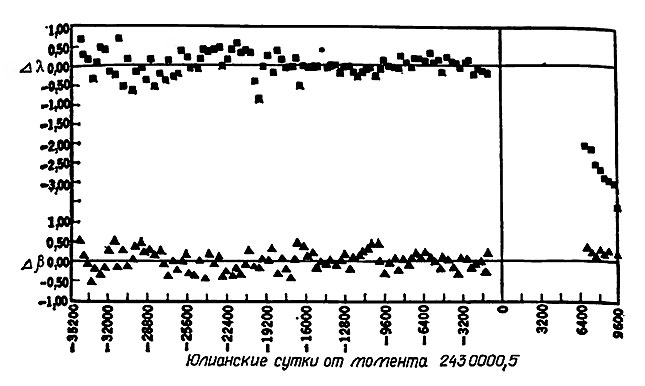
Рис. 5.4. Разности наблюдаемых и вычисленных значений долготы и широты Нептуна для обратного значения массы Плутона, равного 360000
Та же процедура была выполнена для других принятых значений масс. В результате было найдено, что лучше всего согласуется с наблюдениями значение обратной массы 1812000. Окончательная орбита, полученная с этой массой Плутона и построенная по наблюдениям 1846-1938 гг., удовлетворяет наблюдениям 1960-1968 гг. (рис. 5.5).
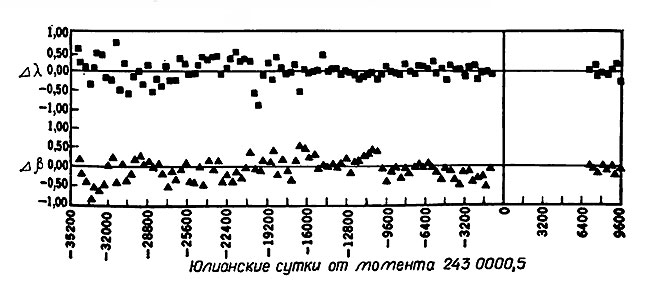
Рис. 5.5. Разности наблюдаемых и вычисленных значений долготы и широты Нептуна для обратного значения массы Плутона, равного 1812000 (Данком, Клепчинский, Сейделмен, 1968 b)
Если плотность Плутона предполагать равной плотности Земли, то новое значение его массы (равное 0,18 массы Земли) приводит к значению диаметра 7200 км. Однако если принять верхнюю оценку 6400 км для диаметра Плутона, найденную Холкдеем и др. (1966), то плотность Плутона должна быть по крайней мере в 1,4 раза больше плотности Земли.
Данком, Клепчинский и Сейделмен заключили, что дальнейшее уточнение массы Плутона и элементов орбиты Нептуна должно быть отложено до завершения обработки наблюдений Нептуна, выполняющейся в Морской обсерватории США.
Холидей (1969) отметил, что значение плотности Плутона предложенное Данкомом и др. (1968а, b) и превышающее плотность Земли в 1,4 раза, является более допустимым, чем гораздо большие значения, предлагавшиеся ранее на основании более высоких оценок массы Плутона. Но даже это более низкое значение близко к плотности железных метеоритов, а такой состав Плутона, по мнению Холидея, несовместим с теориями образования Солнечной системы. Он указал на две причины, ставящие под сомнение определение массы Плутона на основе наблюдений Нептуна:
I) Невязки в долготе могут быть отягчены невыявленными систематическими ошибками.
II) Принятые значения масс Юпитера, Сатурна и Урана также могут быть неточными.
В связи со вторым предположением Холидей заметил, что даже небольшая поправка к значениям масс Сатурна и Урана может оказать влияние на Нептун, достаточное, чтобы привести к еще меньшему значению массы Плутона. Холидей предложил провести вычисление невязок для Нептуна, используя решения с одновременным изменением масс Сатурна, Урана и Плутона.
Данком, Клепчинский и Сейделмен (1970, 1971) повторили свой анализ 1968 г. движения Нептуна на основе того же наблюдательного материала, но с использованием новых обратных значений масс Сатурна и Урана - 3498,7 и 22692 соответственно. Они нашли обратное значение массы Плутона 1900000 (0, 17 массы Земли), что несущественно отличается от их результата 1968 г. (0,18 массы Земли).
Будет очень полезным повторить анализ движения Урана, используя гораздо более точные значения массы Сатурна, полуденные в результате полетов космических аппаратов "Пионер-II", "Вояджер-1" и "Вояджер-2". Позднее можно будет уточнить значения масс Урана и Нептуна, если "Вояджер-2" пройдет мимо этих планет. Однако в настоящее время не планируется никаких космических полетов, которые обеспечили бы непосредственное определение массы Плутона.
Сейделмен, Клепчинский и Данком (1971) подтвердили свое прежнее заключение (Данком, Клепчинский и Сейделмен, 1968а, b), что всякое уточнение значения массы Плутона должно быть отложено до завершения обработки наблюдений Нептуна, проведенных в Морской обсерватории. Они выполнили совместное численное интегрирование орбит пяти внешних планет, используя пересмотренные значения масс Сатурна и Урана (Данком, Клепчинский, Сейделмен, 1970) и ряд значений массы Плутона. Использованные конкретные обратные значения массы Плутона составляли 1812000, 2500000, 3624000 и 5436000. Наилучшим значением массы Плутона считалось то, которое обеспечивало для орбиты Нептуна, построенной по наблюдениям 1846-1938 гг., наилучшее согласие с наблюдениями долготы 1939-1968 гг. Как и следовало ожидать, значения массы Плутона, определенные по наблюдениям различных периодов, оказались весьма противоречивыми. Обратное значение массы, равное 2848000, дало наилучшее решение для наблюдений 1939-1968 гг., в то время как при использовании наблюдений только 1960-1968 гг. наилучшим значением было 3473000. По этой причине Сейделмен и сотрудники решили принять округленное обратное значение массы Плутона, равное 3000000 (0,11 массы Земли), считая его наиболее правдоподобным значением, основанным на всех доступных им данных наблюдений. Это значение массы в комбинации с верхним пре делом 6400 км для диаметра Плутона дает плотность 4,86 г/см3 или 0,88 средней плотности Земли. Если же предполагать плотности Плутона и Земли одинаковыми, то значение диаметра Плутона станет 6112 км.
Эш, Шапиро и Смит (1971) дали сводку наиболее надежных оценок масс всех больших планет. Они обрисовали три главных метода получения таких оценок:
I. Небесно-механические эксперименты с использованием космических аппаратов, пролетающих вблизи планеты.
II. Применение третьего закона Кеплера к наблюдениям периода движения спутника и его среднего расстояния от планеты.
III. Наблюдения резонансных, долгопериодических и короткопериодических эффектов возмущающего действия одной планеты на другую.
Нужно отметить, что метод III был до недавнего времени единственным возможным методом определения массы Плутона, в то время как метод II стал применяться начиная с 1978 г. (Кристи и Харрингтон), а метод I не будет доступен еще достаточно долго. Эш и др. пришли к выводу, что масса Плутона не может быть надежно определена из имевшихся данных с помощью метода III, который в то время был единственно возможным.
Киладзе (1968) предложил определять массу планеты, используя известные значения ее радиуса и периода вращения, с помощью соотношения
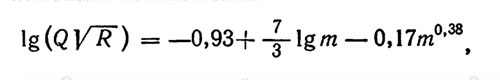
где Q - кинетический момент планеты, R - радиус ее орбиты, а т - масса планеты в единицах массы Земли.
Если Q в формуле выразить через массу, радиус и период вращения планеты, массу выразить через плотность и радиус планеты и подставить уже известные значения радиуса орбиты и периода вращения, то при отбрасывании малых членов получим следующее соотношение:
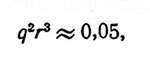
где q - плотность планеты в единицах плотности Земли, r - радиус планеты, выраженный в радиусах Земли.
Киладзе отметил, что поскольку плотность Плутона, вероятно, не превышает плотности Земли, то формула (2) дает нижний предел для радиуса Плутона 0,37. В то же время нижний предел плотности Плутона составляет 0,6 плотности Земли.
Комбинация этих значений приводит к значениям массы Плутона от 0,05 до 0,09 массы Земли. Киладзе рассматривает значение радиуса 0,46 как наиболее вероятное значение, которое соответствует плотности 0,72 (4 г/см3). Результирующая масса Плутона составляет тогда 0,07 массы Земли. Киладзе замечает также, что если период вращения Плутона не равен 6,39 сут (Харди, 1965а), а имеет вдвое большее значение, то тогда масса Плутона составит 0,04 массы Земли. По его заключению, столь малая масса Плутона означает, что возмущения в движении Урана и Нептуна могут быть объяснены только влиянием какого-то неизвестного тела, возможно десятой планеты Солнечной системы.
Камерон (1962) предположил, что в результате конденсации первичного газопылевого облака и образования Солнца и планетной системы на периферии Солнечной системы должна содержаться значительная масса в виде малых твердых частиц. По мнению Уиппла (1964), такая масса может существовать в форме кометного пояса. Этот кометный пояс, слишком слабый для наблюдений с наземными инструментами, может быть обнаружен по его гравитационному влиянию на внешние планеты. По расчетам Уиппла, кометный пояс, содержащий, возможно, от 10 до 20 масс Земли, может существовать на расстоянии от 40 до 50 а. е. от Солнца.
В случае Нептуна предположение о существовании кометного пояса приводит к несколько лучшему уравниванию широтных наблюдений, чем предположение о влиянии возмущений от Плутона. Любое из этих предположений уменьшает сумму квадратов невязок более чем втрое, т. е. довольно существенным образом. Для Урана ни одно из этих предположений не приводит к существенно лучшему уравниванию. Ни одно из предположений не улучшает значительно уравнивания в долготе ни для Урана, ни для Нептуна. Уиппл указывает, что масса Плутона слишком мала для объяснения возмущений в движении Урана и Нептуна и это может служить поддержкой в пользу предположения о существовании кометного пояса за Нептуном.
Сейделмен (1971) исследовал возможность того, что наблюдаемые невязки в движении Урана и Нептуна могут быть объяснены влиянием неизвестной планеты или нескольких планет за Плутоном. Он отметил, что существование такой планеты предполагалось ранее Шютте (1949), Нэфом (1955), Роулинсом (1970) и Ганном (1970). Он использовал программу численного интегрирования, употреблявшуюся Данкомом и его сотрудниками (1968а, b), а также другими исследователями, так как с ее помощью можно было легко учесть влияние дополнительных планет. Сейделмен выбрал три гипотетические планеты: S1, Р1 и Р2. При этом первые две планеты в основном идентичны гипотетическим планетам S и Р, предложенным Пикерингом (1931с), в то время как Р2 - это планета Пикеринга Р, но с более правдоподобным значением массы. Слишком большая масса гипотетической планеты означала бы, что эта планета должна быть достаточно большой и яркой и непременно была бы обнаружена во время систематических поисков Томбо (1961). Томбо пришел к заключению, что возможность существования неоткрытой планеты ярче 16-й звездной величины исключается и что любая планета от 16-й до 17-й величины имела бы хорошие шансы быть обнаруженной. Элементы трех гипотетических планет Сейделмена приведены в табл. 12 (Сейделмен, 1971).
| * | P1 | P2 | S1 |
| Средняя аномалия | 141°26'51,898" | 141°26'51,898" | 141°26'51,898" |
| Аргумент перигелия | 170°30' | 170°30' | 0° |
| Долгота узла | 351° | 351° | 271° |
| Наклон | 37° | 37° | 30°36' |
| Эксцентриситет | 0,265 | 0,265 | 0,0 |
| Большая полуось, а.е. | 75,5 | 75,5 | 48,3 |
| Обратная масса | 7000 | 300000 | 3000000 |
| Оценка звездной величины | 13,6 | 16,1 | 15,7 |
Три гипотетические планеты были по отдельности введены в вычисления со значениями орбитальных элементов, масс и звездных величин, указанными в табл. 12. Результаты интегрирования показывают, что гипотетическая планета Р 1 оказала бы такое сильное возмущающее влияние на внешние планеты, в результате которого невязки увеличились бы, а не уменьшились. Кроме того, такая яркая планета (13,6m) к настоящему времени почти наверняка была бы открыта. Если же масса уменьшалась так, что яркость планеты ослаблялась до допустимого уровня, то она больше не оказывала ощутимого влияния на невязки. Точно так же планета S 1 со звездной величиной, равной 15,7, не влияет существенно на движение внешних планет в течение периода наблюдений. Сейделмен пришел к выводу, что если и есть некоторые свидетельства существования трансплутоновых планет, основанные, в частности, на рассмотрении афелиев ряда семейств комет, то такие планеты должны оказывать незначительное влияние на движение известных планет, за исключением маловероятного случая тесного сближения.
| Аргумент перигелия | 181° |
| Долгота узла | 115,75° |
| Наклон | 120° |
| Эксцентриситет | 0,07 |
| Большая полуось, а. е. | 59,93575 |
| Обратная масса | 90000 |
| Период, годы | 464 |
| Радиус-вектор | 63,491 |
Однако, по утверждению Брэди (1972), нет логических оснований предполагать, что Плутон является самой крайней планетой в Солнечной системе. Поскольку влияние возмущающего тела прямо пропорционально эксцентриситету орбиты возмущаемого тела, трансплутоновая планета возмущала бы объекты с большими эксцентриситетами типа кометы Галлея гораздо более ощутимо, чем большие планеты. Он провел численно-графический эксперимент, чтобы определить, можно ли улучшить предвычисленную орбиту кометы Галлея путем учета влияния гипотетической планеты за Плутоном. Брэди установил, что гипотетическая планета с орбитальными элементами, приведенными в табл. 13 (Брэди, 1972), уменьшила бы невязки во времени прохождения через перигелий кометы Галлея на 93% для орбиты 12а (1910-1456 гг.). Влияние гипотетической планеты на невязки в движении кометы Галлея показано в табл. 14 (Брэди, 1972).
| Год появления | Δ T, сут Орбита 12 а, 9 планет |
Δ T, сут Орбита 52 B, 10 планет |
| 1910 | 0,0 | 0,0 |
| 1835 | 0,0 | -0,8 |
| 1759 | +4,2 | -0,8 |
| 1682 | +8,2 | -3,0 |
| 1607 | +42,6 | -2,7 |
| 1531 | +53,5 | +2,5 |
| 1456 | +49,6 | +3,9 |
Однако для того, чтобы влияние гипотетической планеты на комету стало заметным, комета должна наблюдаться в трех или больше появлениях и иметь достаточно большое афелийное расстояние. При этих условиях можно отделить искомый эффект от ошибок наблюдений. Только две кометы - комета Ольберса и комета Понса - Брукса - удовлетворяют этим условиям. Орбиты этих комет интегрировались подобно орбите кометы Галлея с учетом и без учета гипотетической планеты. Влияние планеты явственно сказывается в уменьшении невязок в табл. 15 (Брэди, 1972).

Таблица 15. Невязки в движении комет Ольберса и Понса-Брукса с учетом и без учета влияния трансплутоновой планеты (Брэди. 1972)
Планета, существование которой постулировал Брэди, должна двигаться вокруг Солнца на удвоенном расстоянии Нептуна по орбите с наклоном 120°. Ее гипотетическая масса в три раза больше массы Сатурна, а вероятный блеск этой планеты соответствует 13-й или 14-й звездной величине. Как такая планета могла избежать обнаружения при поисках Томбо? Брэди указывает, что в течение 16-летнего периода поисков с 1929 по 1946 г. вся траектория планеты лежала вне области, охваченной поисками (рис. 5.6) (Брэди 1972).
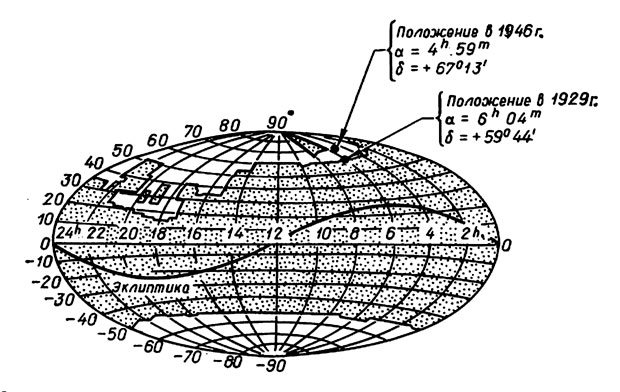
Рис. 5.6. Область, охваченная поиском транснептуновой планеты в Ловелловской обсерватории в 1929-1945 гг. (темная область). Положения гипотетической трансплутоновой планеты показаны на 1929 и 1946 гг. (Брэди, 1972)
Фосс, Шейв-Тейлор и Уитворт (1972) провели фотографические поиски гипотетической планеты Брэди (1972) в области, простирающейся по крайней мере на 3,5° в любом направлении от предвычисленного положения. С помощью 33-сантиметрового астрографа Гринвичской обсерватории были сняты две серии пластинок с минимальным интервалом в одни сутки между парами пластинок. Предсказанное суточное движение планеты на пластинках составляло 0,7 мм. Каждая пластинка исследовалась на блинк-компараторе до звездной величины, равной по крайней мере 15,5, а в большинстве случаев - до 16,0. Фосс, Шейв-Тейлор и Уитворт не обнаружили никакого движущегося объекта ярче указанной величины ни на одной паре пластинок. Они пришли к заключению, что если трансплутоновая планета существует, то она либо значительно менее массивна и, следовательно, существенно слабее, чем предсказал Брэди, либо она не находится вблизи указанного Брэди положения.
Харди (1965а, b) выполнил новую серию фотоэлектрических наблюдений Плутона, используя 60-сантиметровый сейфертовский рефлектор Дайеровской обсерватории. Ему удалось получить уточненное значение синодического периода вращения, равное 6,38673 сут, или 6 сут 9 ч 16 мин 54±26 с, которое может отличаться от сидерического или истинного периода вращения на ±45 с. Эта неточность обусловлена незнанием ориентации оси вращения Плутона и направления его вращения. Данные Харди указывают на некоторое уменьшение средней яркости Плутона по сравнению с измерениями 1955 г. Результат Харди (1965а) находится в противоречии с визуальными оценками яркости Плутона Мосли (1969), который получил среднее значение визуальной звездной величины 14,0 из наблюдений с 25-сантиметровым рефрактором обсерватории Арма.
Харди (1969) приписал изменение в звездной величине Плутона изменению в характере его поверхности и, следовательно, его альбедо. Плутон стал ближе к Солнцу по сравнению со своим средним гелиоцентрическим расстоянием 5864 млн. км. Харди предположил, что вследствие этого возможный снежно-ледяной покров Плутона, состоящий из замерзшего азота, растаял и это привело к снижению его отражательной способности. Такой фазовый переход может объяснить потускнение Плутона в течение предыдущего десятилетия, а также вариации его блеска с периодом 6,39 сут (обусловленные циклом день/ночь - таяние/замерзание).
Лацис и Фикс (1972) провели фурье-анализ кривой блеска Плутона с целью исследования распределения по долготе ярких и темных областей поверхности Плутона. Хотя было ясно, что существует заметная разница в альбедо между светлыми и темными областями, не удалось определить, обусловлено ли изменение блеска темными или же светлыми зонами и являются ли эти зоны большими или сравнительно малыми. Однако авторы считают, что если два типа областей поверхности имеют различные поляризационные свойства и если изменение поляризации в функции от фазы может быть измерено, то природа поверхности Плутона будет определена более надежно. Лацис и Фикс указывают также, что гипотеза пятнистой поверхности позволяет лучше объяснить кривую блеска Плутона, чем предположения о несферической форме Плутона или о большом наклоне его оси вращения.
Андерссон (1973), используя UBN-наблюдения Плутона, сделанные в 1972 г. в обсерватории Мак-Дональд и в лаборатории Луны и планет США, вычислил среднее значение звездной величины, эквивалентное значению V= 15,15 для среднего расстояния в противостоянии. Первоначальные определения Уокера и Харди (1955) дали значение 14,90. Андерссон указал альтернативное объяснение этого различия, предположив, что ось вращения Плутона лежит в плоскости орбиты; ось была направлена к Земле в 1930 г. во время открытия планеты. Согласно этой модели, отражательная способность полярной шапки Плутона должна почти вдвое превышать отражательную способность его экваториальной области.
Фикс, Неф и Килей (1970) измерили относительную яркость Плутона на 21 равноотстоящих длинах волн между 3400 и 5900 Å. На основе этих измерений и нормализованного солнечного спектра они определили относительное альбедо Плутона на каждой длине волны (рис. 5.7). Они нашли, что альбедо Плутона обнаруживает общее увеличение к красной области спектра с пиком около 3800 Å и явным падением в районе 4900 Å.
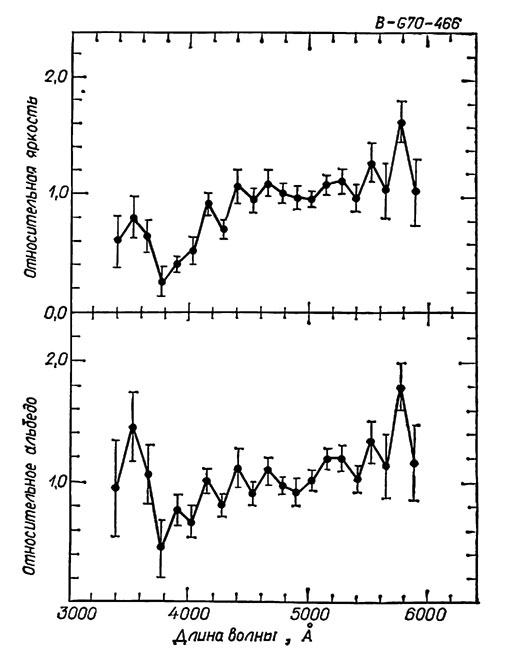
Рис. 5.7. Зависимость относительной яркости и относительного альбедо Плутона от длины волны (Фикс, Неф, Килей, 1970)
В работе Мэннинга (1971), подобно более ранней работе Холидея (1969), отмечается, что, согласно теории первичной вращающейся туманности, Плутон в силу своего положения в Солнечной системе не может быть планетой, богатой железом. Однако Мэннинг обращает внимание на значительное сходство в общем характере и деталях между спектром отражения Плутона, полученным Фиксом, Нефом и Килей (1970), и спектром поглощения земных силикатов, содержащих железо (рис. 5.8). Мэннинг отмечает, например, корреляцию между минимумом спектральной кривой Плутона при 3780 Å и выделяющейся линией поглощения вблизи 3700 Å в спектрах минералов. Он заключил, что имеется достаточная корреляция по положению и полуширине полос в спектрах Плутона и земных кристаллов для оправдания его предположения об обильном присутствии железа на поверхности Плутона.
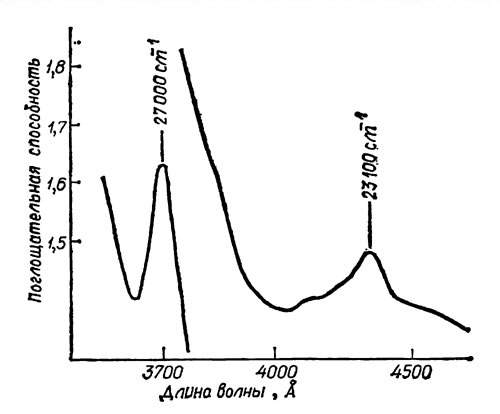
Рис. 5.8. Спектры поглощения земных гроссуларов - гранатов при 293 К Мэннинг, 1971)
В. Вебстер, А. Вебстер и Дж. Вебстер (1972) сделали попытку обнаружения теплового радиоизлучения Плутона с помощью интерферометра с 26-метровой антенной Национальной радиоастрономической обсерватории. Однако ни на одной из двух использованных длин волн - 11,1 см (2,695 ГГц) и 3,7 см - (8,085 ГГц) им не удалось зафиксировать излучение от Плутона. Наблюдения на волне 8,085 ГГц дали верхний предел 162° К для температуры диска Плутона на волне 3,7 см.
Согласно Рубашевскому (1966), первым, кто еще в 1941 г. говорил о возможности определения диаметра Плутона из наблюдений покрытий на нескольких обсерваториях, был польский астроном Банахевич. Банахевич ошибочно оценил, что Плутон покрывает звезды ярче 15-й фотографической величины в среднем раз в году и высказал предположение, что визуальные наблюдения этих событий возможны с помощью телескопов с 30-50-сантиметровой апертурой. Безуспешные попытки Кордылевского (1956-1958) обнаружить какие-либо покрытия вызвали у него сомнения в справедливости оценок частоты покрытий, полученной Банахевичем.
Холидей (1963) предложил новый способ определения диаметра Плутона путем наблюдения покрытия звезды на двух или нескольких обсерваториях. Он указал два возможных пути согласования малого значения диаметра Плутона, измеренного Койпером (1950), со значением массы, необходимой в качестве причины предполагаемых возмущений от Плутона в движении Урана и Нептуна; комбинация этих значений дает неправдоподобное значение средней плотности планеты порядка 50 г/см3. Во-первых, Холидей предположил, что ошибка может быть приписана неверному определению массы, по необходимости основанному на старых наблюдениях. Если для средней плотности предположить более разумное значение 4 г/см3, то масса Плутона составит только 0,07 массы Земли, что сравнимо с массой Меркурия или самых больших спутников Юпитера, Сатурна и Нептуна. Альтернативное решение Холидей видел в признании ошибочности измерения диаметра. Согласно более ранней работе Альтера (1952), видимый диаметр Плутона может представлять собой только нижний предел истинного диаметра, если отражательная способность поверхности такова, что при наблюдении с большого расстояния кажется освещенной лишь центральная область. Такое потемнение к краю действительно наблюдалось Харди (1965b). При рассмотрении этих двух возможных объяснений Холидей отметил, что ошибка в определении диаметра более существенно влияет на среднюю плотность, чем ошибка в массе, так как плотность зависит от куба диаметра и лишь от первой степени массы.
Альтер (1952) пришел к заключению, что, по-видимому, измерить истинный диаметр можно пока лишь при покрытии звезды Плутоном, но даже в этом случае, по его мнению, потребуются наблюдения многих покрытий. Определив сначала, что измерение продолжительности покрытия не представляет серьезной проблемы, Холидей (1963) предположил, что одного покрытия достаточно для определения точного значения диаметра Плутона. Это объясняется тем, что Земля и Плутон имеют сравнимые размеры, и поэтому параллакс при наблюдении Плутона из двух обсерваторий составляет существенную долю углового диаметра Плутона. Вследствие этого будет наблюдаться разная продолжительность покрытия на двух обсерваториях. Указанный эффект заметен даже при малом расстоянии между двумя обсерваториями. Для почти центральных покрытий (происходящих вдоль диаметра Плутона) продолжительность будет примерно одинаковая, но само это равенство доказывает почти центральный характер покрытия, и, следовательно, на каждой обсерватории будет измеряться истинный диаметр Плутона.
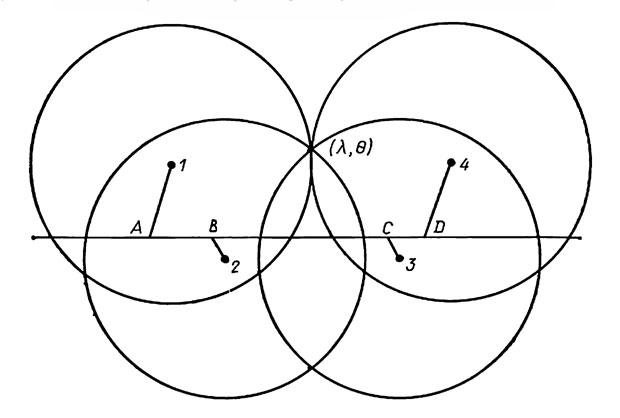
Рис. 5.9. Геометрическая картина покрытия, наблюдаемого из двух обсерваторий, иллюстрирующая эффекты параллакса (Холидей, 1963)
Принцип метода, согласно описанию Холидея (1963), проиллюстрирован на рис. 5.9 в предположении, что на двух обсерваториях наблюдается полное покрытие. Сначала нанесем изображение (в сильно увеличенном масштабе) траектории Плутона на небе, как она была бы видна из центра Земли. Отметим точки А, В, С, D на этой траектории, где А и D - положения в моменты исчезновения и появления звезды, наблюдаемые из одной обсерватории, а B и С - соответствующие точки для второй обсерватории. Эти положения могут быть найдены интерполированием из эфемерид Плутона. Относительное расположение точек А, В, С, D нужно знать с большой точностью, но этого не требуется для расчета всей траектории на небесной сфере. Используя стандартные формулы, приводимые в астрономических ежегодниках, вычислим геоцентрический параллакс в прямом восхождении и склонении для каждой обсерватории и нанесем видимые положения центра Плутона (точки 1, 2, 3, 4), соответствующие геоцентрическим положениям (А, В, С, D). При этом учитываются долгота и широта обсерваторий, а также вращение Земли; кроме того, в формулы входят известное расстояние Плутона от Земли и диаметр Земли. Продолжительность покрытия, наблюдаемого в первой обсерватории (положения 1 и 4), довольно большая и соответствует более центральному покрытию, чем наблюдаемое из второй обсерватории (положения 2 и 3).
Обозначим радиус Плутона через R. Тогда четыре окружности, каждая с радиусом R и с центрами в точках 1, 2, 3, 4, должны все пройти через положение покрываемой звезды. Обозначим координаты звезды через (λ, θ), а координаты четырех известных центров через (х1, у1) и т. д. Тогда можно написать четыре уравнения вида
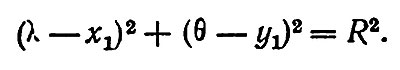
Комбинируя любые три из этих уравнений, мы можем найти λ, θ и R, т. е. положение покрываемой звезды относительно Плутона и диаметр Плутона. Четвертое уравнение служит контролем.
Заметим, что в принципе требуется только три уравнения, поэтому в случае двух обсерваторий можно получить решение, даже если одно исчезновение или появление не наблюдались из-за облачности или другой помехи. В случае трех подходящим образом расположенных обсерваторий для получения решения достаточно трех наблюдений исчезновения звезды (Холидей, 1963).
По оценке Холидея, средняя частота покрытий составляет от 0,16 покрытий в год для звезд с визуальной величиной, равной 14, до 1,24 покрытий в год для звезд с визуальной величиной, равной 19. Возможно, эти значения должны быть уменьшены в два или три раза, если учитывать неблагоприятные положения планет и погодные условия. Тем не менее Холидей пришел к выводу, что подходящие покрытия происходят каждые несколько лет и, учитывая желательность точного определения диаметра Плутона, следует организовать службу предвычисления покрытий для обсерваторий.
В период времени после внесения Холидеем (1963) предложения о наблюдении покрытий до первой фактической попытки такого наблюдения, предпринятой двумя годами позже, Харди (1965b) опубликовал данные, свидетельствующие о том, что диаметр Плутона существенно больше значения 5900 км, установленного Койпером (1950). Эти данные были основаны на фотометрических наблюдениях 1964 г., которые выявили кривую блеска в основном того же вида, что и ранее, но с несколько большей амплитудой (Уокер, Харди, 1955). Кривая блеска показывает усиление блеска Плутона в течение четырех суток, а затем его резкое ослабление в течение двух суток во время каждого периода вращения, составляющего 6 сут 9 ч 16 мин 54±26 с. Такая кривая блеска указывает на то, что Плутон имеет наибольшую яркость в центре со значительным потемнением к краю.
В соответствии с предложением Холидея была осуществлена программа измерения траектории Плутона среди слабых опорных звезд на пластинках, снятых 120-сантиметровым шмидтовским телескопом Паломарской обсерватории и 60-сантиметровым сейфертовским телескопом Дайеровской обсерватории. Положения звезд измерялись на блинк-компараторе Манна в Оттавской обсерзатории. Далее использовалась небольшая вычислительная программа для определения минимального расстояния между Плутоном и звездами, лежащими вблизи его предвычисленной траектории, совместно с указанием времени наиболее тесного сближения. Возможное покрытие звезды с визуальной величиной 15,3 было предсказано в ночь с 28 на 29 апреля 1965 г. (Холидей, 1965а). Объявляя о предсказанном покрытии, Холидей указал, что суммарный блеск Плутона и звезды с координатами α= llh 23m 12,1s, δ = 19°47'32" (1950) будет соответствовать звездной величине 13,8. Таким образом, если бы покрытие действительно произошло, блеск должен был резко упасть до значения 14,1 звездной величины, соответствующего Плутону. Результирующее 25%-ное изменение яркости было бы доступно наблюдениям на телескопах с диаметром свыше 50 см. В этой попытке фиксировать ожидаемое покрытие участвовали фактически все обсерватории Северной Америки, обладающие телескопами с соответствующей апертурой и подходящими фотометрами. По широте эти обсерватории простирались от Виктории в Британской Колумбии до Форта Дэвиса в Техасе.
К сожалению, никакого покрытия не наблюдалось. Край полосы покрытия прошел чуть южнее самой южной из участвовавших в наблюдениях обсерваторий - обсерватории Мак-Дональд.
Однако в итоговых отчетах Холидея (1965b) и Холидея, Харди, Франца и Прайзера (1966) отмечалось, что удалось получить крайнюю верхнюю границу в 6800 км для диаметра Плутона. Результаты этой наблюдательной программы были представлены в работе 1966 г. диаграммой, приводимой на рис. 5.10. Положение звезды на этом рисунке отмечено точкой; сплошная линия изображает фотоцентрическую траекторию Плутона на расстоянии 0,143" от звезды. Минимальное фотоцентрическое расстояние для обсерватории Мак-Дональд составляло 0,125", соответствуя диаметру Плутона 5800 км для касательного покрытия. Круг изображает проекцию диска планеты, видимого в обсерватории Мак-Дональд при значении диаметра Плутона 5500 км. При оценке средней ошибки 0,013" можно установить крайний верхний предел для диаметра 6800 км. Таким образом, значение Койпера 5900 км, хотя и не подтвержденное непосредственно, оказывается заключенным между новым верхним пределом 6800 км и нижним пределом 2000 км; последнее значение диаметра соответствует единичному альбедо. Верхний предел 6800 км соответствует крайнему нижнему пределу для альбедо Плутона 0,1. Комбинируя значение диаметра 6800 км с наиболее высоким разумным значением плотности 5,5 г/см3 (плотность Земли), получаем пересмотренный верхний предел массы Плутона 0,14 массы Земли, или 2 200000 для обратного отношения к массе Солнца. Даже это максимальное значение массы Плутона недостаточно, чтобы вызвать возмущения в движении Урана и Нептуна, использовавшиеся при определении массы и предсказании существования Плутона. Поскольку, как указали Холидей и др. (1966), надежно установлено, что диаметр Плутона значительно меньше диаметра Земли, описанный выше параллактический эффект может дать еще большую точность и в конечном итоге диаметр Плутона может быть определен с точностью до 1%. Сандерс (1965) опубликовал результаты попыток наблюдать покрытия в Ликской обсерватории с помощью 90-сантиметрового рефрактора и 300-сантиметрового рефлектора.
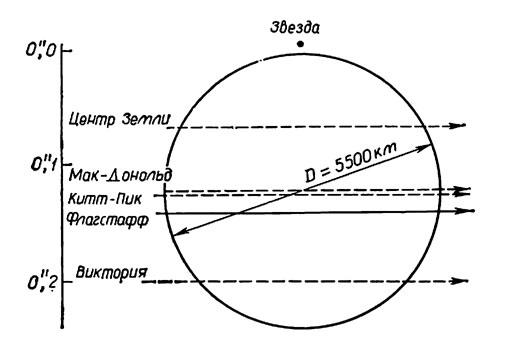
Рис. 5.10. Представление фотоцентрической траектории Плутона, проходящего мимо звезды (Холидей и др., 1966)
Рубашевский (1966) наметил программу наблюдения покрытий, аналогичную программе Холидея (1963). Эта программа отличается в основном методикой предвычисления покрытий звезд Плутоном и содержит более пессимистические оценки частоты таких покрытий. Он указал на желательность наблюдения покрытий звезд Плутоном с помощью баллонов или спутников, пока не будут созданы такие околоземные обсерватории, как 240-сантиметровый космический телескоп, намечаемый к выводу на орбиту по программе Спейс Шаттл в конце 1983 г.* По его мнению, в результате работы Холидея (1965b) стало очевидным, что источник противоречия между массой и размерами Плутона заключается в очень неточном определении массы планеты из теории возмущений, а не в "квазизеркальном" характере отражения солнечного света от поверхности Плутона, как считалось ранее (Харди, 1965b). Рубашевский заключил, что противоречие с массой Плутона происходит, вполне возможно, из-за неучета в его движении эффектов, вызываемых гипотетической трансплутоновой планетой.
* (Ряд работ, посвященных техническим аспектам и научной программе Космического Телескопа опубликован в журнале Celestial mechanics, 22, № 2, 1980. - Прим. ред.)
О'Лири (1972) призвал к организации систематической и широкой программы предвычисления покрытий с учетом в случае Плутона звезд до 18-й фотографической величины включительно. Он отметил, что в силу коротких времен упреждения (порядка нескольких недель) для наблюдения более частых покрытий более слабых звезд требуется кооперирование между обсерваториями, располагающими подходящими инструментами. Он оценил, что количество "подходящих" покрытий звезд Плутоном, а именно таких покрытий, где интенсивность света падает более чем на 10%, составляет по крайней мере одно в год. Интересно отметить, что Барбиери, Капаччиоли и Пинто (1975) сообщили о почти-покрытии Плутоном звезды 17-й величины на пластинке, снятой 25 мая 1974 г. с помощью телескопа Шмидта в обсерватории Азиаго.
|
ПОИСК:
|
© ADEVA.RU, 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://adeva.ru/ 'Энциклопедия небесных тел'
При использовании материалов сайта активная ссылка обязательна:
http://adeva.ru/ 'Энциклопедия небесных тел'